4.4 Korteste stier
Korteste veje.
En kantvægtet, rettet graf er en rettet graf, hvor hver kant er udstyret men en vægt eller omkostning. En korteste vej fra knude \(s\) til knude \(t\) er en rettet vej fra \(s\) til \(t\) med den egenskab, at ingen anden sådan vej har en lavere vægt.
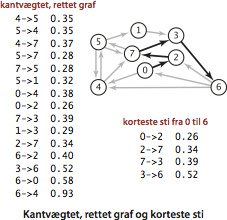
Egenskaber.
Vi sammenfatter flere vigtige egenskaber og antagelser:- Veje er rettede.
En korteste vej skal respektere kanternes retning.
- Vægte er ikke nødvendigvis afstande.
Geometrisk intuition kan være nyttigt, men kantvægtene kan
repræsentere andet end afstand, fx rejsetid eller omkostninger.
- Ikke alle knuder behøver at være tilgængelige.
Hvis \(t\) ikke kan nås fra \(s\), er der ingen vej
overhovedet, og derfor er der ingen korteste vej fra \(s\) til
\(t\).
- Negative vægte giver komplikationer.
I første omgang antager vi, at alle kantvægte er positive eller
nul.
- Korteste veje er normalt simple.
Vores algoritmer ignorere nulvægtskanter, der danner kredse,
således at de fundne korteste vej er simple.
- Korteste veje er ikke nødvendigvis unikke.
Der kan være flere veje af den laveste vægt mellem et par af knuder;
vi er tilfredse med at finde nogen af disse veje.
- Parallelle kanter og løkker kan findes. I teksten antager vi, at grafen ikke har parallelle kanter, og bruger notation v-> w for at angive kanten fra \(v\) til \(w\), men vores programmer håndterer parallelle kanter uden problemer.
Datatype for kantvægtet, rettet graf.
Vi repræsenterer de vægtede kanter ved hjælp af følgende APG:
| public class DirectedEdge implements Comparable<Edge> | ||
|---|---|---|
| Edge(int v, int w, double weight) | skab en rettet kant fra v til w med vægt weight | |
| double | weight() | denne kants vægt |
| int | from() | knuden, denne kant peger fra |
| void | to() | knuden, denne kant peger på |
| String | toString() | tekstuel repræsentation af kanten |
Metoderne from() og to() angiver kantens endepunkter. Programmet DirectedEdge.java implementerer denne APG.
Vi repræsenterer kantvægtede, rettede grafer ved hjælp af følgende APG:
| public class EdgeWeightedDigraph | ||
|---|---|---|
| Graph(int V) | skab en rettet graf med V knuder og ingen kanter | |
| Graph(In in) | læs en rettet graf fra indputstrømmen in | |
| int | V() | antal knuder |
| int | E() | antal kanter |
| void | addEdge(DirectedEdge e) | tilføj kanten e til denne graf |
| Iterable<DirectedEdge> | adj(int v) | kanter som peger fra v |
| Iterable<DirectedEdge> | edges() | alle kanter i denne graf |
| String | toString() | tekstuel repræsentation af grafen |
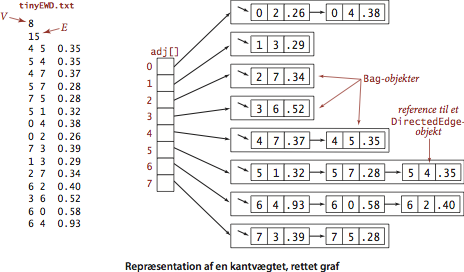
APG for korteste veje.
Vi bruger følgende APG til at beregne korteste veje i en kantvægtet, rettet graf:
| public class SP | ||
|---|---|---|
| SP(EdgeWeightedDigraph G, int s) | konstruktør | |
| double | distTo(int v) | afstand fra \(s\) til \(v\), eller \(\infty\) hvis ingen sti findes |
| boolean | hasPathTo(int v) | findes en sti fra \(s\) til \(v\)? |
| Iterable≤DirectedEdge> | pathTo(int v) | en sti fra \(s\) til \(v\), eller null hvis ingen sti findes |
- tinyEWD.txt indeholder 8 knuder og 15 kanter
- mediumEWD.txt indeholder 250 knuder og 2.546 kanter
- 1000EWG.txt indeholder 1.000 knuder og 16,866 kanter
- 10000EWG.txt indeholder 10.000 knuder og 123,462 kanter
- largeEWG.txt indeholder en million knuder og 15,172,126 kanter.
Datastruktur for korteste veje med enkelt kilde.
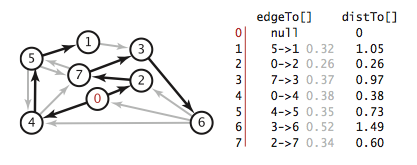
Betrat en kantvægtet, rettet graf \(G\) og en startknude \(s\). Et korteste-veje-træ er en delgraf indeholdene \(s\) og alle knuder, der kan nås fra \(s\), der danner et rettet træ rodfæstet i \(s\), hvori hver vej er en korteste vej i \(G\).Vi repræsenterer de korteste-veje med to knude-indekserede rækker:
- kanter i korteste-veje-træet : edgeTo
[v] angiver den sidste kant på en korteste vej fra \(s\) til
\(v\).
- Afstand fra startknuden : distTo [v] er længden af en korteste vej fra \(s\) til \(v\).
Slækning.
Vores algoritmer for korteste veje er baseret på en operation kaldet slækning . Vi sætter først distTo[s] til 0 og distTo[v] til uendeligt for alle andre knuder \(v\).- Slække en kant
For at slække en kant v-> w undersøger vi, om vi
kan forbedre den bedst kendte vej fra \(s\) til \(w\) ved at gå
fra \(s\) til \(v\), og derefter følge kanten v-> w.
I bekræftende fald opdaterer vi datastrukturerne.
private void relax(DirectedEdge e) { int v = e.from (), w = e.to (); if (distTo [w]> distTo [v] + e.weight ()) { distTo [w] = distTo [v] + e.weight (); edgeTo [w] = e; } }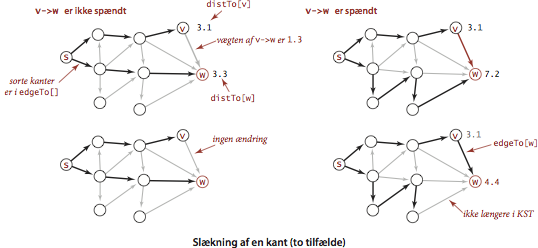
- Slække en knude.
Alle vores algoritmer slækker faktisk alle kanter, der peger
fra samme knude.
private void relax(EdgeWeightedDigraph G, int v) { for (DirectedEdge e: G.adj (v)) { int w = e.to (); if (distTo [w]> distTo [v] + e.weight ()) { distTo [w] = distTo [v] + e.weight (); edgeTo [w] = e; } } }
Påstand. (Optimalitet af korteste veje)
Lad \(G\) være en kantvægtet, rettet graf med startknude \(s\). Antag, at for hver knude \(v\), der kan nås fra \(s\), angiver distTo[v] er længden af nogen sti fra s til v . For hver knude \(v\), der ikke kan nås fra \(s\), er distTo[v] lig med uendeligt. Disse værdier er længden af korteste stier hvis og kun hvis de opfylder distTo [w] <= distTo [v] + e.weight () for hver kant \(e\) = v-> w. Optimalitetsbetingelserne leder til en generel algoritme til at finde korteste veje. For øjeblikket begrænser vi os til ikke-negative vægte.
Påstand. (Generel algoritme for korteste veje)
Sæt først distTo [s] til 0, og alle andre afstande i distTo [] til uendelig. Fortsæt med at slække en vilkårlig kant i \(G\), indtil der ikke er flere kanter, der kan slækkes. Herefter gælder for hver knude \(v\), der kan nås fra s , at afstanden i distTo [v] angiver længden af en korteste vej fra s til v , og værdien af edgeTo[] er den sidste kant på denne vej.
Dijkstras algoritme.
Sæt først dist [s] til 0 og alle andre indgange i distTo [] til uendeligt. Begynd med et tomt træ. Vælg en knude uden for træet med laveste afstand i distTo[], føj den til træet, og slæk den. Fortsæt indtil alle knuder er i træet eller ingen knude uden for træet har en endelig afstand i distTo[].Programmet DijkstraSP.java er en effektiv implementation af Dijkstras algoritme. Den bruger prioritetskøen fra IndexMinPQ.java.
Påstand.
Dijkstras algoritme finder korteste veje fra en enkelt kilde i en kantvægtet rettet med ikke-negative vægte i ekstra plads proportional med \(V\) og tid proportional med \(E\log V\) i værste fald.
Kantvægtede, acycliske, rettede grafer.
Vi bruger forkortelsen KRAG for kantvægtet, rettet, acyklisk graf.- Korteste stier fra enkelt kilde i KRAG.
Vi betragter nu en algoritme til at finde korteste veje i KRAG, der er enklere og hurtigere
end Dijkstras algoritme.
- Den finder korteste stier fra en enkelt kilde i lineær tid.
- Den håndterer negative kantvægte.
- Det løser beslægtede problemer, såsom at finde længste stier.
Algoritmen kombinerer knudeslækning med topologisk sortering. Vi initialiserer distTo [s] til 0 og alle andre indgange i distTo [] til uendelig. Derefter slækker vi alle knuder én efter én i topologisk orden. Programmet AcyclicSP.java implementerer denne fremgangsmåde. Det bygger på en version af Topological.java , udvidet til at behandle kantvægtede, rettede grafer.
- Den finder korteste stier fra en enkelt kilde i lineær tid.
- Længste stier fra enkelt kilde i KRAG.
Vi kan finde længste stier fra en enkelt kilde i KRAG
ved at initialisere alle indgange i distTo [] til minus
uendeligt og vende uligheden i slækningsmetoden relax () .
Programmet AcyclicLP.java implementerer
denne fremgangsmåde.
- Kritiske stier.
Vi betragter nu planlægninsproblemet med forrangskrav på
parallelle processorer.
Givet er en mængde af opgaver af bestemt varighed med forrangkrav der
angiver at visse opgaver skal være afsluttet, inden visse andre
opgaver kan påbegyndes.
Hvordan kan vi planlægge opgaverne på identiske processorer (så mange
som nødvendigt), således at de opgaver er udført inden for korteste
tid og alle krav respekteres?
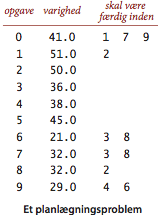
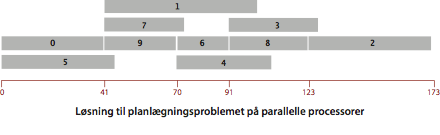
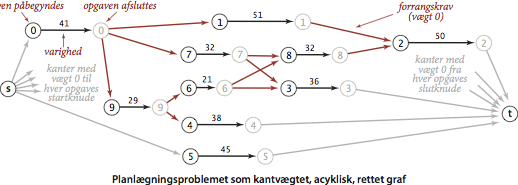
Dette problem kan løses ved at formulere det som en længste-stier-problem i en KRAG: Opret en graf med en kilde \(s\), et dræn \(t\), og henholdsvis en startknude og en slutknude per opgave. For hver opgave tilføjes en kant fra startknuden til slutknuden med vægt svarende til opgavens varighed. For hvert forrangskrav v->w tilføjes en kan med vægt nul fra \(v\)s slutknude til \(w\)s startknude. Endelig tilføjes kanter med vægt nul fra kilden til hver opgaves startknude og fra hver opgaves slutknude til drænet.
Nu kan hver opgave planlægges på tidspunktet givet ved længden af den længste sti fra kilden.
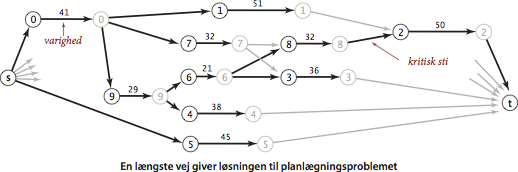
Programmet CPM.java implementer denne algoritme.
Påstand.
Ved at slække knuder i topologisk orden kan vi finde korteste og længste stier fra en enkelt kilde i en KRAG i tid proportional med \(E + V\).
Korteste veje i kantvægtede rettede grafer.
- Negative kredse.
En negativ kreds er en rettet kreds, hvis samlede
vægt (summen af kantvægtene) er negativ.
Bemærk at begrebet »korteste vej« er meningsløs i en graf, som
indeholder en negativ kreds.
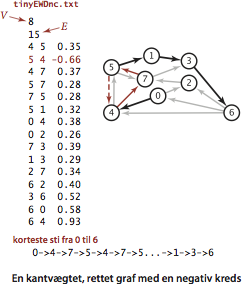
Vi betragter nu kantvægtede rettede grafer uden negative kredse.
- Bellman-Fords algoritme.
Initialisér distTo [s] til 0 og alle andre
indgange i distTo [] til uendeligt.
Slæk nu alle grafens kanter i vilkårlig rækkefølge.
Gentag dette \(V\) gange.
Vi betragter ikke denne version i større detalje, fordi det altid afspænder \(V E\) kanter.for (int pass = 0; pass < G.V(); pass++) for (int v = 0; v
- Købaseret Bellman-Ford.
De eneste kanter, hvis slækning kan føre til en ændring i
distTo[], peger væk fra knuder, hvis distTo[]-værdi blev
ændres i det forrige gennemløb.
Vi kan holde sådanne knuder i en kø.
Programmet BellmanFordSP.java
implementerer denne fremgangsmåde ved at opretholde yderligere to
datastrukturer:
- En kø af knuder, der skal slækkes.
- En knude-indiceret boolsk række onQ[], der angiver, om en givet knude er i køen, for at undgå dubletter.
- En kø af knuder, der skal slækkes.
- Finde negative kredse.
I mange applikationer vil vi finde negative kredse.
Derfor tilføjer vi følgende metoder til vores APG:
boolean hasNegativeCycle() har grafen en negativ kreds? Iterable<DirectedEdge> negativeCycle() en negativ kreds, eller null hvis ingen sti findes - Finde arbitrage.
Som en eksempel på en naturlig forekomst af negative kredse,
betragt et marked for finansielle transaktioner, fx valutaer.
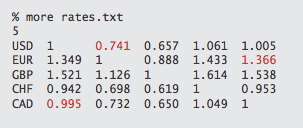
Tabellen i rates.txt viser
omregningskurserne blandt nogle valutaer.
Den første linje i indput er antallet \(V\) af valutaer.
Derefter følger en linje per valuta, som indeholder valutaens navn
efterfulgt af omregningskurser til de øvrige valutaer.
En mulighed for arbitrage er en rettet kreds således at
produktet af de valutakurser er større end 1.
For eksempel siger vores tabel, at 1000 amerikanske dollars vil købe
1000 × 0,741 = 741 euro, så vi kan købe 741 × 1,366 = 1012,206
canadiske dollars med vores euro, og endelig 1012,206 × 0,995 =
1007,14497 dollars med vores canadiske dollars, en profit på 7,14497 dollar!
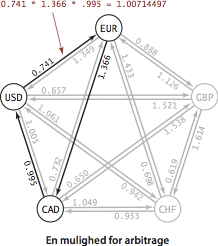
For at formulere arbitrageproblemet i termer af at finde negative kredse, erstatter vi hver vægt med dens logaritme , negeret. Herved svarer produktet \( w_1w_2\cdots w_k\) kantvægtene på en sti i det oprindelige problem til summen \( -\ln w_1 -\ln w_2 \cdots-\ln w_k\) af kantvægtene i det transformerede problem. Produktet er større end 1 hvis og kun hvis summen er negativ. Programmet Arbitrage.java implementerer denne idé.
Påstand.
Der findes en korteste vej fra \(s\) til \(v\) i en kantvægtet, rettet graf hvis og kun hvis der findes mindst én rettet sti fra \(s\) til \(v\) og ingen knude på nogen rettet sti fra \(s\) til \(v\) er på en negativ kreds.
