3.4 Spredetabeller
Når nøglerne er små heltal, findes der en implemention af symboltabeller som er overordentlig enkel: Datastrukturen er en række af samme størrelse som den størst mulige nøgle; nøglerne tolkes som rækkeindices sådan at værdien knyttet til nøgle \(i\) gemmes i rækkens \(i\)’te plads. I dette afsnit betragter vi en metode kaldt spredning, som bruger denne idé for mere komplekse typer af nøgler ved at transformere nølger til rækkeindices gennem aritmiske operationer.
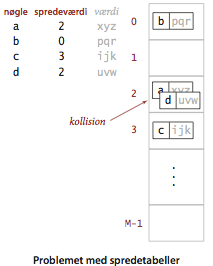
Spredningsbaserede søgealgoritmer består af to dele.
Den først del er en spredefunktion.
Denne bruges til beregning af søgenøglens spredeværdi, som vil
blive brugt som rækkeindeks.
Idealet er at forskellige nøgler resulterer i forskellige indices.
Dette ideal kan generelt ikke opnås, fordi der er flere mulige nøgler
en spredeværdier.
Derfor må vi tage højde for, at to eller flere søgenøgler kan spredes
til samme rækkeindeks.
Spredesøgningens anden del er derfor en konvention for
kollisionshåndtering.
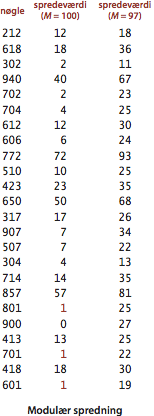
Spredefunktioner.
Hvis vores række har plads til \(M\) nøgle-værdi-par, behøver vi en funktion, der kan transformere en given nøgle til et indeks i rækken, dvs. et heltal mellem \(0\) og \(M-1\). Vores ønske til en spredefunktion er, at den kan beregnes effektivt og at den spreder nøglerne uniformt i intervallet \(\{0,\ldots, M-1\}\).- Typisk eksempel. Betragt en anvendelse hvor nøglerne er US-amerikanske sygesikringsnumre som fx 123-45-6789, et nicifret tal opdelt i tre felter. Nummerets første felt angiver det geografiske område, hvor sygesikringsnummeret blev udstedt. For eksempel er numre som begynder med 035 fra Rhode Island, og numre som begynder med 214 er fra Maryland. De følgende to felter identificerer personen. Der er en milliard forskellige sygesikringsnumre, men vi forestiller os en anvendelse, hvor kun nogle få hundrede nøgler skal behandles, som vi vil gemme i en spredetabel af størrelse \(M = 1000\). Det ligger lige for at bruge sygesikringsnummerets første tre cifre som spredeværdi. Det er imidlertid en dårlig ide, fordi vores tænkte database muligvis indeholder mange poster fra samme geografiske område; fx studerende ved et bestemt universitet eller kunder i en bestemt butik. Derfor er det bedre at tage sygesikringsnummerets sidste tre cifre som spredeværdi. Endnu bedre er det at opfatte alle ni cifre som et stort heltal og beregne spredeværdien baseret på dette, som beskrevet i det følgende.
- Positive heltal. Den mest brugte metode for a sprede heltal kaldes modulær spredning: Vælg en rækkestørrelsen \(M\) som et primtal og beregn for hver heltalsnøgle \(k\) værdien \(k\mod M\), dvs. resten ved heltalsdivision af \(k\) med \(M\). Denne funktion er meget nem at beregne (i java bruges udtrykket k % M) og spreder nøgler jævnt og effektivt mellem \(0\) og \(M-1\).
- Kommatal. Når nøglerne er reelle tal mellem \(0\) and \(1\), er vi fristet til at gange med \(M\) og afrunde til nærmeste heltal for at få en spredeværdi mellem \(0\) og \(M-1\). Problemet med denne metode er, at nøglens mest betydende cifre bliver for vigtigte, og de mindste betydende cifre spiller ingen rolle overhovedet. En bedre måde er at bruge modulær spredning på nøglens binærrepræsentation. Java gør netop dette.
- Strenge.
Modulær spredning virker også for meget lange nøgler som fx strenge,
ved at betragte dem som kæmpeheltal.
Den følgende kodestump beregner en modulær spredeværdi hash
for strengen \(s\):
int hash = 0; for (int i = 0; i < s.length(); i++) hash = (R * h + s.charAt(i)) % M; - Sammensatte nøgler.
Hvis nøgletypen består af flere heltalsfelter, kan vi blande disse
felter på samme måde, som vi lige så for strenge.
Antag fx at søgenøglen er et amerikansk telfonnummer af af typen USPhoneNumber.java, som består af
tre heltalsfelter area (trecifret områdenummer),
exch (trecifret centralnummer) og ext (firecifret
abonnentnummer).
I dette eksempel kan vi beregne spredeværdien som
int hash = (((area * R + exch) % M) * R + ext) % M;
- Konventioner i programmeringssproget java. Java understøtter behovet for spredefunktioner for hver datatype ved at kræve, at hvert objekt implementerer en metode som returnerer objektets spredekode hashCode(), et heltal på 32 bits. For hvert objekt skal spredekoden hashCode() være konsistent med lighedsmetoden equals. Det vil sige at hvis udtrykket a.equals(b) er sandt, så skal spredekoden a.hashCode() være den samme som spredekoden b.hashCode(). Den omvendte implikation holder ikke: To objekter med samme spredekode kan være forskellige. Vi kan da bruge javas indbyggede lighedsmetode equals() til at afgøre objektlighed.
- Konvertering af spredekode til rækkeindeks. Endeligt
skal vi konvertere 32-bits heltallet til et passende rækkeindeks.
Vi kombinerer objektets spredekode med modulær spredning for at få et
heltal mellem \(0\) og \(M-1\) som følger:
Koden maskerer fortegnsbitten, hvilket omvandler et 32-bits-heltal til et 31-bits ikke-negativt heltal, og beregner resten ved division med \(M\), på samme måde som i modulær spredning.private int hash(Key key) { return (key.hashCode() & 0x7fffffff) % M; } - Brugerdefinerede spredekoder. Klientkode forventer, at spredekoden hashCode() fordeler nøglerne uniformt blandt alle mulige 32-bits heltal. Med andre ord forventer vi for hvert objekt x at udtrykket x.hashCode() i princippet giver hver af de \(2^{32}\) mulige 32-bits-værdier med samme sandsynlighed. Javas implementation hashCode() prøver at opnå denne opførsel for mange af de grundlæggende typer (inklusive String, Integer, Double, Date og URL), men for en brugerdefineret type skal man gøre det selv. Programmet PhoneNumber.java illustrerer en mulig tilgang: Lav instansvariablerne om til heltal og brug modulær spredning. Programmet Transaction.java illustrerer en endnu enklere tildgang: brug hver instansvariabels hashCode() til at konvertere dem til hver sin 32-bits-heltalsværdi af typen int og udfør beregningerne på resultatet.
- Den skal være deterministisk, dvs. at samme nøgler skal producere samme spredeværdi.
- Den skal kunne beregnes effektivt.
- Den skal sprede nøglerne uniformt.
Antagelse J (uniform spredning).
Spredefunktionen fordeler nøgler uniformt og uafhængigt i \(\{0,\ldots,M-1\}\).Spredning med separat hægtning.
Spredefunktionen omvandler nøgljer til rækkeindices. Spredningsalgoritmens anden komponent er kollisionshåndteringen: en strategi der angiver, hvad der sker, når to nøgler spreded til samme indeks. En enkel løsning er at bygge en hægtet liste af nøgle-værdi-par i hver rækkeindgang, hvor der opstår en kollision. Vi vælger rækkestørrelsen \(M\) til at være tilstrækkelig stor for at listerne bliver tilstrækkelig korte til at blive gennemsøgt effektiv. For at slå op i datastrukturen beregner vi først søgennøglens spredeværdi, betragter den tilsvarende rækkeindgang og gennemløber den hægtede liste sekventielt, til vi finder nøglen.
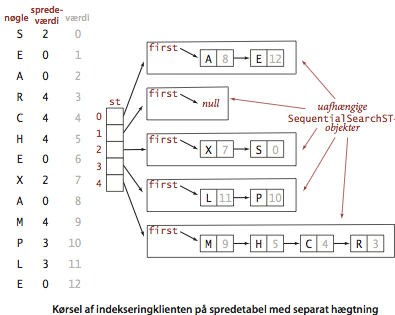
Programmet SeparateChainingHashST.java implementerer en symboltabel ved brug af en spredetabel med separat hægtning. Den opretholder en række, hvis indgange er symboltabeller implementeret som uordnede hægtet lister SequentialSearchST. Opslagsmetoden get() og indsættelsesmetoden put() beregner først en spredeværdi til at bestemme den symboltabel, der potentielt indeholder søgenøglen, og bruger så metoderne get() og put() fra SequentialSearchST for at udføre operationen.
Påstand K. Betragt en spredetabel med separat hægtning af \(M\) lister. Hvis tabellen indeholder \(N\) nøgler under antagelse J, så er sandsynligheden for at længden af en liste er inden for en lille konstant faktor af \(N/M\) meget tæt på 1.
Dette klassiske matematiske resultat virker besnærende, men det afhænger fuldstændigt af antagelse J. I praksis ser man dog ofte samme opførsel.
Egenskab L. Betragt en spredetabel med separat hægtning af \(M\) lister, som indeholder \(N\) nøgler. Antallet af sammenligninger ved indsættelse og forgæves søgning er proportional med \(N/M\).
Spredning med lineær probering.
Et alternativ til separat hægtning er at gemme \(N\) nøgle-værdi-par i en række af størrelse \(M> N\) og stole på, at der er tilstrækkelig mange tomme rækkeindgange til at håndtere kollisioner. Denne ide kaldes åben adressering. Den enkleste implementation af åben adressering er lineær probering: Hvis en søgenøgles spredeværdi angiver en rækkeindgang, som allerede er optaget af en anden nøgle, anbringer vi den givne nøgle i rækkens næste ledige plads ved lægge 1 til det indeks, det gives af spredeværdien. Der er tre mulige scenarier:- Vi finder søgenøglen på den nye plads: Søgningen lykkedes.
- Rækkens plads er tom, dvs. at den indholder nulreferencen: Søgenøglen findes ikke, søgning er forgæves.
- Rækkeindgangen indeholder en anden nøgle end søgenøglen: Prøv næste indgang.

Programmet LinearProbingHashST.java implementerer en symboltabel ved brug af en spredetabel med lineær probering.
Som ved separat hægtning afhænger køretiden af metoder baseret på åben adressing af forholdet \(\alpha = N/M\), men med en anden fortolkningen. Ved separat hægtning angiver \(\alpha\) den gennemsnitlige listelængde og er generelt større end 1. Ved åben adressering angiver \(\alpha\) andelen af optagede rækkeindgange; den skal være mindre end 1. Vi kalder \(\alpha\) for spredetabellens belastning.
Påstand M. Betragt en spredetabel af størrelse \(M\), der bruger lineær probering for \(N = \alpha M\) nøgler. Under antagelse J er det gennemsnitlige antal prober \(\sim\frac{1}{2} (1 + 1 / (1 - \alpha))\) for vellykket søgning og \(\sim\frac{1}{2} (1 + 1 / (1 - \alpha)^2)\) for indsættelse og forgæves søgning.
Gøgespredning.
En anden implementation af åben adressering er gøgespredning: I gøgespredning bruges to spredefunktioner \(h_1\)og \(h_2\) i stedet for én. Hver søgenøgle har altså to spredeværdier; som invariant fastholder vi, at hver søgenøgle \(x\) befinder sig i en af de to rækkeindgange, som indiceres af henholdsvis \(h_1(x)\) og \(h_2(x)\). Søgning kræver altså blot to opslag i værste fald. En ny søgenøgle indsættes i den rækkeindgang, der er angivet af nøglens første spredeværdi. Hvis denne rækkeindgang allerede er optaget af en anden søgenøgle, skubbes denne ud af indgangen og indsættes på sin alternative plads. Her kan den selv skubbe en tredje søgenøgle ud, og så videre, til en ledig plads er fundet eller processen går i ring. I det senere tilfælde vælges to nye spredeværdier og hele tabellen bygges på ny.
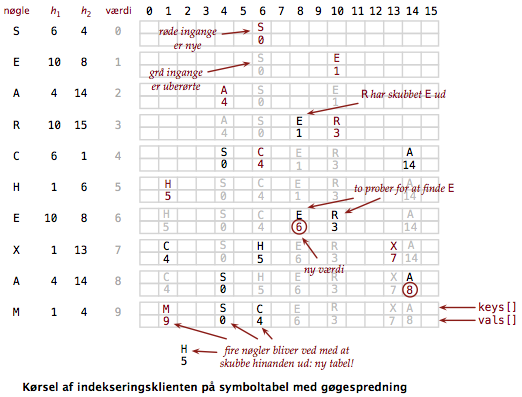
Påstand. Betragt en spredetabel af størrelse \(M\), der bruger gøgespredning for \(N = \alpha M\) nøgler og antag at begge spredefunktioner opfylder antagelse J om uniform spredning og er uafhængige. Køretiden for søgning er konstant i værste fald. Køretiden for indsættelse er forventet konstant hvis \(\alpha < \frac{1}{2}\).
