3.1 Symboltabeller
Symboltabeller.
En symboltabel er en datastruktur der knytter en værdi til en entydig nøgle. Datastrukturen understøtter to grundlæggende operationer: at indsætte et nyt nøgle-værdi-par i tabellen og at søge efter en givet nøgle (eller slå nøglen op) og returnere den tilknyttede værdi.Symboltabeller bruges i mange sammenhænge, nogle eksempler er vist i følgende tabel:
| anvendelse | formål for søgning | nøgle | værdi |
|---|---|---|---|
| ordbog | finde definition | opslagsord, lemma | definition |
| bogindeks | finde relevante sider | emneord | liste af sidenumre |
| kontohåndtering | behandling af transaktioner | kontonummer | transaktionsdetaljer |
| websøgemaskine | finde relevante websider | søgeord | liste af sidenavne |
| compiler | finde type og værdi | variabelnavn | type og værdi |
Abstrakt datatype for symboltabeller.
Følgende APG beskriver de grundlæggende opererationer for symboltabeller.
| public class ST<Key, Value> | ||
|---|---|---|
| ST() | en tom symboltabel | |
| void | put(Key key, Value val) | indsæt nøgle-værdi-parret. Fjern nøglen hvis val er null. |
| Value | get(Key key) | værdien knyttet til den givne nøgle key, eller null hvis nøglen ikke findes. |
| void | delete(Key key) | fjern den givne nøgle (samt den tilknyttete værdi). |
| boolean | contains(Key key) | findes den givne nøgle? |
| boolean | isEmpty() | er symboltabellen tom? |
| int | size() | antallet af nøgle-værdi-par |
| Iterable<Key> | keys() | alle nøgler |
For at skikre at vores implementationer er konsistente, kompakte og anvendlige, vedtager vi nogle generelle konventioner for symboltabeller.
- Generiske typer. Vi bruger generiske datatyper for både nøgler og værdier.
- Nøgledubletter. Symboltabllen indeholder ingen nøgledubletter: hver nøgle er knyttet til præcis én værdi. Hvis klienten indsætter et nøgle-værdi-par i en symboltabel der allerede indeholder den samme nølge, så erstatter den givne værdi den gamle værdi der var knyttet til nøglen. Denne konvention definerer abstraktionen associativ række, hvor vi kan opfatte symboltabellen som en række hvis nøgler svarer til indices og hvis værdier svarer til rækkeindgange.
- Værdien nul. Ingen nøgle kan nogensinde knyttes til nulværdien null. Denne konvention hænger sammen med specifikationen i APG’en, hvor vi bestemmer at opslagsmetoden get() skal returnere null for nøgler som ikke er i symboltabellen. Konventionen har to (bevidste) konsekvenser: For det første kan vi afgøre om symboltallen indeholder et givet nøgle-værdi-par, ved at se om opslagsmetoden get() returnerer null. For det andet kan vi bruge indsættelsesmetoden put() med nulværdien null som værdiargument til at fjerne et nøgle-værdi-par.
- Fjernelse. Der er to måder for fjernelse i end symboltabel: I sløv fjernelse knytter vi den nøgle, vi vil fjerne, til nulværdien null. Muligvis rydder vi op ved et senere tidspunkt ved at fjerne alle den slags nøgler. I ivrig fjernelse fjerner vi nøglen med det samme. Den foroven nævnte indsættelse put(key, null) er altså en sløv implementation af fjernelsen delete(key). Vi vil senere give en ivrig implementation af fjernelsesmetoden delete(), der erstatter den sløve løsning.
- Iteratorer. Metoden keys() returnerer en generisk gennemløber Iterable<Key> som giver klienter adgang til hele symboltabellens indhold.
- Nøglelighed.
Programmeringssproget java kræver, at alle objekter implementerer en
lighedsmetode equals(), og stiller en sådan til rådighed for
de grundlæggende typer som Integer, Double og
String samt for mere komplekse typer som Date,
File og URL.
For anvendelser der bruger en af disse datatyper som nøgle, kan vi
bruge denne indbyggede lighedsmetode.
Hvis fx x og y er værdier af strengtypen
String, så er udtrykket x.equals(y) sandt hvis og kun
hvis x og y har samme længde og indeholder samme
tegn på hver plads.
I praktikken er nøgler ofte mere komplicerede, som fx objekter af
klassen Person.java.
Sådanne klient-definerede nøgletyper overlagrer lighedsmetoden
equals().
Ifølge javas konventioner skal equals() implementere en
ækvivalensrelation:
- refleksiv: x.equals(x) er sand.
- symmetrisk: x.equals(y) er sand hvis og kun hvis y.equals(x) er sand.
- Transitiv: hvis x.equals(y) og y.equals(z) begge er sande, så er x.equals(z) også sand.
Derudover skal metoden equals() kunne tage grundklassen Object som argument og opfylde de følgende krav:
- Konsistens: gentagne kald af formen x.equals(y) skal retunere samme værdi, så længe hverken ojektet x eller argumentet y er ændret.
- Ej nul: udtrykket x.equals(null) er falsk.
For at kunne sikre konsistens anbefales det at gøre nøgletypen Key uforanderlig.
Ordnede symboltabeller.
I mange anvendelser er nøgler sammenlignelige, dvs. at nøgleobjekterne opfylder kravene i grænsefladen Comparable. I så fald kan nøglerne a og b. sammenlignes med udtrykket a.compareTo(b). Mange symboltabeller udnytter den implicitte ordning af nøglerne som er givet af grænsefladen Comparable til effektive implementationer af operationerne put() og get(). Når symboltabellens nøgler er ordnene, så kan vi udvide APG’en med en række naturlige og nytte funktioner, der tager udgangspunkt i nøglernes indbyrdes ordning.
| public class ST<Key extends Comparable<Key>, Value> | ||
|---|---|---|
| ST() | en tom symboltabel | |
| void | put(Key key, Value val) | indsæt nøgle-værdi-parret. Fjern nøgle hvis val=null. |
| Value | get(Key key) | værdien knyttet til nøglen key, eller null hvis nøglen ikke findes. |
| void | delete(Key key) | fjern den givne nøgle (og værdien knyttet til den). |
| boolean | contains(Key key) | er den givne nøgle knyttet til en værdi? |
| boolean | isEmpty() | er symboltabellen tom? |
| int | size() | antallet af nøgle-værdi-par |
| Key | min() | mindste nøgle |
| Key | max() | største nøgle |
| Key | floor(Key key) | gulvet, dvs. største nøgle mindre end eller lig med den givne nøgle key |
| Key | ceiling(Key key) | loftet, dvs. mindste nøgle større end eller lig med den givne nøgle key |
| int | rank(Key key) | rangen, dvs. antallet af nøgler skarpt mindre end den givne nøgle key |
| Key | select(int k) | nøglen af rang r |
| void | deleteMin() | fjern mindste element |
| void | deleteMax() | fjern største element |
| int | size(Key lo, Key hi) | antal nøgler i intervallet [lo..hi] |
| Iterable<Key> | keys(Key lo, Key hi) | alle nøgler i intervallet [lo..hi], i sorteret orden |
| Iterable<Key> | keys() | alle nøgler |
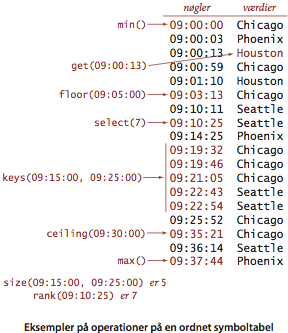
- Minimum og maksimum. Symboltabellens minimum og maksimum er hhv. dens minste og største nøgle. Vi har tidligere mødt denne funktionalitet i forbindelse med prioritetskøer, som vi altså kan opfatte som ordnede symboltabller med indsættelse og minimumsopslag. (Bemærk dog at vi i vores konventioner for prioritetskøer tillader nøgler af samme værdi.)
- Gulv og loft. En given nøgles gulv er den største nøgle i symboltabellen som er mindre end eller lig med den givne nøgle. En given nøgles loft er den mindste nøgle i symboltabellen, der er større end eller lig med den givne nøgle. Terminologien kommer fra de tilsvarende funktioner for reelle tal, der afrunder henvoldsvis ned eller op til nærmeste heltal.
- Rangering og selektion. En nøgles rang angiver dets placering i den sorterede sekvens af alle nøgler. Rangen er altså antallet af nøgler i symboltabellen, der er mindre end eller lig med den givne nøgle. Ved selektion forstår vi den tilsvarende operation, der vælger nøglen af givet rang.
- Intervalopslag. Hvor mange nøgler falder inden for et givet interval? Hvilke nøgler falder inden for et givet interval? Metoderne size() og keys() med to argumenter besvarer disse spørgsmål og har mange anvendelser fx i store databaser.
- Fjernelse af minimum og maksimum. Programmeringsgrænsefladen for ordnede symboltabeller tilbyder metoder for fjernelse af den minimale og maskimale nøgle og deres tilknyttede værdier.
- Randvilkår. Som konvention returnerer vi nulværiden null i situationer, hvor en metode skal returnere en nøgle, som ikke findes. For eksempel vil min(), max(), floor() og ceiling() returnere null hvis symboltabellen er tom, og metoden select(k) returnerer null hvis k er mindre end 0 eller skarpt større end size(). Vi bestemmer også at fjernelserne deleteMin() og deleteMax() ikke har nogen effekt på en tom symboltabel, hvilet er konsistent med vore konvention at fjernelsen delete() er effektløs, når den givne nøgle ikke findes i symboltabellen.
- Konsistens af nøglelighed. Det anbefales i java at gøre sammenligningsmetoden compareTo() konsistent med lighedsmetoden equals() i alle sammenlignelige typer. Det vil sige at en klasse der implementerer sammenligningsgrænsefladen Comparable, skal sikre at der for hvert par af objekter a og b gælder at udtrykkene (a.compareTo(b) == 0) og a.equals(b) har samme værdi.
Eksempelklienter.
Vi betragter to klienter: en testklient, som skal køre vores implementationer på små indput, og en klient til at måle tidsforbrug.- Testklient. Programmet TestST.java læser en sekvens af strenge fra standardindput, bygger en symboltabel der knytter værdien \(i\) til den \(i\)’te indputnøgle, og endeligt udskriver hele symboltabellen.
- Frekvenstæller. Programmet FrequencyCounter.java er en symboltabelklient, der finder antallet af forekomster af hver streng (af en vis længde) i en sekvens af strenge fra på standardindput. Derefter gennemløbes alle nøgler for at finde den hyppigst forekommende streng.
Sekventiel søgning i en uordnet hægtet liste.
Programmet SequentialSearchST.java implementerer APG’en for (ikke-ordnede) symboltabeller ved brug af en hægtet liste af knuder, der indeholder nøgler og værdier. For at implementere opslaget get(), gennemsøger vi hele listen og bruger equals() til at sammenligne søgenøglen med nøglerne i hver knude. Hvis vi finder en knude men den søgte nøgle, returnerer vi knudens værdi, ellers returnerer vi nulværdien null. For at implementere indsættelsen put(), gennemsøger vi ligeledes hele listen og bruger equals() til at sammenligne den givne med nøglerne i hver knude. Hvis vi finder en knude med den givne nøgle, ændrer vi knudens værdi til den givne værdi. Ellers skaber vi en ny knude med den givne nøgle og værdi og hægter den i starten af listen. Denne metode kaldes sekventiel søgning.
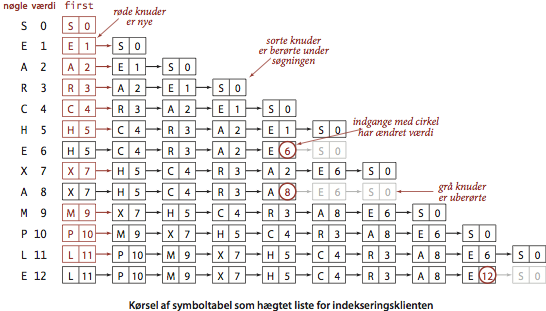
Påstand A.
Betragt en symboltabel implementeret som uordnet hægtet liste af \(N\) elementer. Indsættelse og forgæves søgning bruger \(N\) sammenligninger. Vellykket søgning bruger \(N\) sammenligninger i værste fald. Specielt bruger indsættelse af \(N\) nøgler i en oprindeligt tom datastruktur \(\sim\frac{1}{2}N^2\) sammenligninger.Binærsøgning i en ordnet række
. Programmet BinarySearchST.java implementerer programmeringsgrænsefladen for ordnede symboltabeller. Datastrukturen består af to korresponderende rækker for henholdvis nøgler og værdier, sådan at nøglerne står i sorteret orden. Implementationen baserer sig på rangeringsmetoden rank(), som giver antallet af nøgler mindre end eller lig med den givne nøgle. For opslaget get() giver rangen præcis den givne nøgles position i den sorterede nøglerække, hvis den findes. For indsættelsen put() finder rangen præcis den værdi i værdirækken, der skal opdateres, hvis nøglen allerede findes. Ellers angiver rangen den position, hvor begge rækker skal udvides med det givne nøgle-værdi-par. Hertil skal alle større rækkeindgange flyttes en position til højre for at give plads; flytningen implementeres lettest fra højre til venstre.
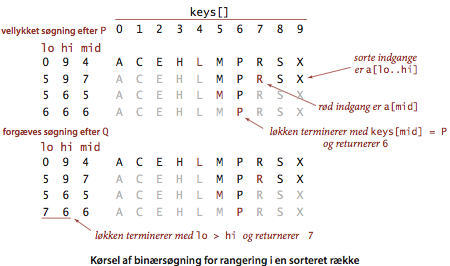
- Binærsøgning.
Anledningen til at holde nøglerne in sorteret række er at vi kan bruge
rækkeopslag til en dramatisk forbedring af antallet af sammenligninger
for hver søgning.
Hertil bruges en ærværdig, klassisk algoritme kaldet
binærsøgning.
Grundidéen er enkel: Vi afgrænser den del af rækken som kan
indeholde søgenøglen.
For at finde søgenøglen sammenligner vi den med delrækkens midterste
indgang.
Hvis søgenøglen er skarpt mindre end midternøglen, fortsætter vi
søgningen i venstre halvdel.
Hvis søgenøglen er skarpt større end midternøglen, fortsætter vi
søgningen i højre halvdel.
Ellers er søgenøglen lig med midternøglen.

- Øvrige operationer. Fordi nøglerne holdes i en sorteret række, kan de fleste ordningsrelaterede operationer implementeres enkelt og kompakt.
