2.3 Kviksortering
Kviksortering blev opdaget af Tony Hoare i 1960. Den er en populær sorteringsalgoritme, fordi den er enkel at implementere, opfører sig godt på mange forskellige slags data og er væsentlig hurtigere end andre sorteringsmetoder i typiske anvendelser. Kviksortering bruger ingen ekstra plads bortset fra rekursionsstakken, tager gennemsnitligt tid proportional med \(N\log N\) for at sortere \(N\) elementer og har en usædvanlig kort indre løkke.Grundideen for kviksortering.
Kviksortering er ligesom flettesortering en del-og-hersk-metode. Den virker ved først at opdele rækken i to dele, som siden sorteres rekursivt, hver for sig.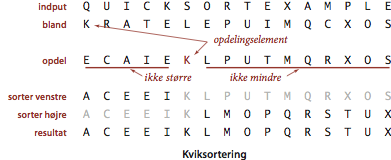
- For noget j gælder at indgangen a[j] er på sin endelige plads i den sorterede række.
- Ingen indgang fra a[lo] til og med a[j-1] er større end a[j].
- Ingen indgang fra a[j+1] til og med a[hi] er mindre end a[j].
Opdeling.
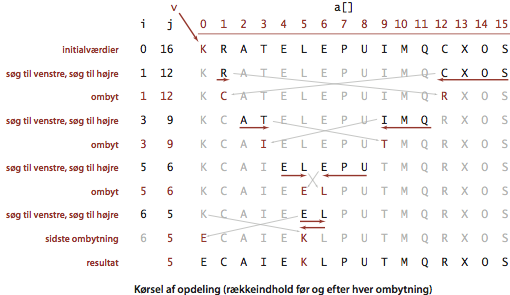
Vi betrager nu opdelingsmetoden. Vi begynder med vilkårlig at udnævne elementet a[lo] til opdelingselement, dvs. det element, der straks anbringes i sin endelige position. Derefter afsøger vi rækken fra dens venstre ende indtil vi finder et element, der er større end eller lig med opdelingselementet. Samtidigt afsøger vi rækken fra dens højre ende indtil vi finder et element, der er mindre end eller lig med opdelingselementet.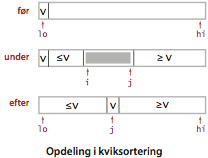
Kviksortering.
Programmet Quick.java implementerer kviksortering ved brug af opdelingsmetoden foroven.
Implementationsdetaljer.
Det er værd at lægge mærke til en række subtile detaljer i forbindelse med vores implementation af kviksortering.- Opdeling på plads. Det er nemt at implementere opdelingen ved brug af en ekstra række, men ikke så meget lettere, at det er værd den ekstraomkostning, der ligger i at kopiere den opdelede række tilbage til originalet.
- Randvilkår. Når rækkens mindste eller største elementer bliver valgt som opdelingselement skal vi passe på at indicerne XXX lo og hi ikke løber ud over henholdsvis rækkens højre og venstre ende.
- Tilfældighed. Den indledende tilfældige blanding sætter rækkens elementer i tilfældig ordning. Idet alle elementerne i delrækkerne behandles ens, har implementationen Quick.java den egenskab, at alle delrækker ligeledes er tilfældige. Denne omstændighed er central for at algoritmen opfører sig forudsigeligt. En alternativ måde er at vælge et tilfældigt element som opdelingselement i metoden partition().
- Terminering af løkken. Det er ikke helt ligetil at afgøre, om indicerne lo og hi har krydset hinanden. En gængs fejl er at overse, at rækken kan indeholde flere nøgler med samme værdi som opdelingselementet.
- Behandling af elementer med samme nøgle som opdelingselementet. Det er bedst at afbryde venstre gennemsøgning, når man møder en nøgle, der er større end eller lig med opdelingselements, og at afbryde højre gennemsøgning, når man møder en nøgle, der er mindre end eller lig med opdelingselementets. Selvom denne konvention virker til at skabe unødvendige ombytninger af elementer med samme nøgle som opdelingselementets, er den nødvendig for at undgå kvadratisk køretid i visse situationer.
- Terminering af rekursionen. En gængs fejl ved implementationen af kviksortering opstår, når opdelingselementet sendes længere ned i rekursionen sammen med en af delrækkerne. Det fører til en uendelig rekursiv løkke, når opdelingselementet er rækkens mindste eller største element.
Påstand.
Kviksortering bruger \(\sim 2 N \ln N\) sammenligninger (og en sjettedel så mange ombytninger) i gennemsnit for at sortere en række af længde \(N\) med forskellige nøgler.Påstand.
Kviksortering bruger \(\sim~ N^2/2\) sammenligninger i værste fald. Den indledende tilfældige blanding af rækken sikrer, at det værste fald indtræffer med forsvindende lille sandsynlighed.Køretidens standardafvigelse er omtrent \(0,65 N\), så køretiden går mod gennemsnittet som \(N\) vokser og er tæt på gennemsnittet med høj sandsynlighed. Sandsynligheden af, at kviksortering bruger et kvadatrisk antal sammenligninger ved sortering af en stor række, er betydeling mindre, end at maskinen under kørslen bliver ramt af lynet.
Forbedringer.
Kviksortering er siden tresserne blevet analyseret og forbret af mange forskere.- Afskæring til indsættelsessortering. Det kan ofte betale sig at skifte til indsættelsessortering for meget korte delrækker, som vi allerede så ved flettesortering. Det optimale værdi for afskæringen er systemafhængig, men værdier mellem 5 og 15 virker i mange sammenhænge.
- Mediansopdeling. En anden måde at forbedre kviksorterings køretid er at lade opdelingselementet være medianen af en lille mængde af rækkeelementer. På denne måde finder man et lidt bedre opdelingselement, men betaler med omkostningen for at beregne medianen. Det viser sig, at man kan få en ganske god forbedring allerede ved at vælge medianen af bare tre tilfældigt valgte elementer.
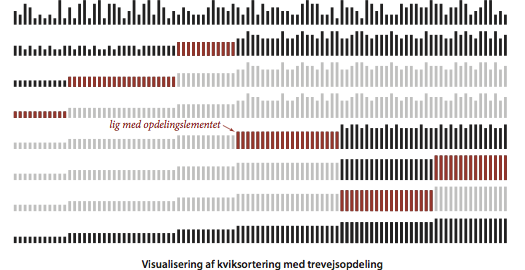
Visualisering.
Programmet QuickBars.java visualiserer en opførslen af kviksortering ved brug af både opdeling efter medianen af 3 og afskæring til indsættelsessortering for små delrækker.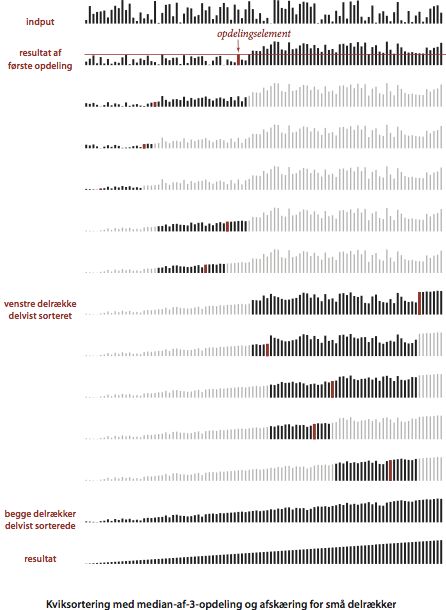
Entropioptimal sortering.
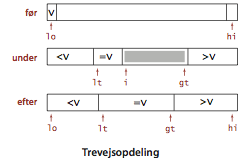
I mange anvendelser møder man rækker, hvor samme sorteringsnøgle forekommer mange gange. I sådanne situationer kan man muligvis nedbringe køretiden fra linearitmisk til lineær.En oplagt ide er at dele rækken i tre dele, afhængigt af om elementerne er skarpt mindre en, lig med, eller skarpt større end opdelingselementet. Dette er en klassisk programmeringsopgave, som blev populariseret af E. W. Dijkstra som det hollandske flagproblem: Opdelingen af en række med tre forskellige nøgler minder om farverne i det hollandske flag.
Dijkstras løsning baserer sig på et enkelt rækkegennmenløb fra
venstre til højre, som opretholder tre pegere: En peger
lt således at alle elementer i a[lo..lt-1] er mindre
end v; en peger gt således at alle elementer i
a[gt+1..hi] er større end v, og en peger
i således at alle elementer i a[lt..i-1] er lig med
I begyndelsen er i lig med lo.
Herfra sammenlignes a[i] og v med
trevejssammenligningen fra grænsefladen
Comparable. Der er tre tilfælde:
Programmet Quick3way.java
implementerer kviksortering med trevejsopdeling.
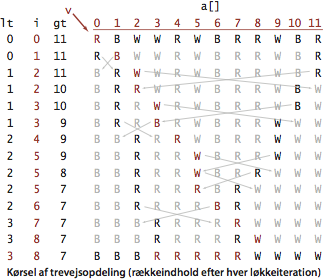
Påstand.
Kviksortering med trevejsopdeling er entropioptimal.
Visualisering.
Programmet Quick3wayBars.java visualiserer
opførslen af kviksortering med trevejsopdeling.