1.5 Eksempel: Forén og find
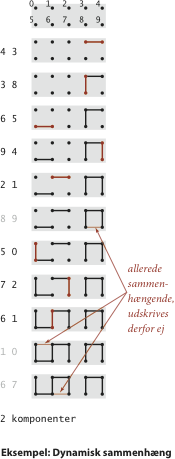
Dynamisk sammenhæng
Betragt følgende problem: Indput er en sekvens af heltalspar. Hvert heltal repræsenterer et objekt af en eller anden slags, fx en person i et socialt netværk, et kontaktpunkt i et elektrisk kredsløb, et variabelnavn i et program eller en position i en krystal. Den ønskede fortolkning af parret p q er, at objektet p forbindes med objektet q. Vi antager, at «er forbundet med» opfylder kravene til en ækvivalensrelation:
- Symmetri: Hvis p er forbundet med q, så er q forbundet med p.
- Transitivitet: Hvis p er forbundet med q, og q er forbundet med r, så er p forbundet med r.
- Refleksivitet: p er forbundet med p.
Vores mål er at skrive et program som fjerner overflødige par fra sekvensen: Det indlæste heltalspar p q skal kun rapporteres, hvis p og qs sammenhæng ikke allerede er givet af tidligere indlæste par. Ellers skal programmet ignorere parret p q og fortsætte med at indlæse det næste par af heltal.
APG forén-og-find.
Følgende programmeringsgrænseflade indkapsler de grundlæggende opererationer for den abstrakte datype forén-og-find. Den opretholder en unikt komponentnavn for hver komponent. I begyndelsen tilhører hvert element sin egen komponent.
| public class UF | ||
|---|---|---|
| UF(int A) | \(N\) elementer med heltalsnavne fra \(\{0,\ldots,N-1\}\) uden forbindelser | |
| void | union(int p, int q) | tilføj forbindelse mellem \(p\) og \(q\) |
| int | find(int p) | komponentnavn for \(p\) (en værdi i \(\{0,\ldots, N-1\}\)) |
| boolean | connected(int p, int q) | tilhører \(p\) og \(q\) samme komponent? |
| int | count() | antal komponenter |
For at teste den abstrakte datatype løser metoden main() i
UF.java det dynamiske sammenhængsproblem.
Der er tre filer med testdata: Filen tinyUF.txt
indeholder de 11 forbindelser fra det lille eksempel øverst til højre,
filen mediumUF.txt indeholder 900 forbindelser
og filen largeUF.txt
indeholder millioner af forbindelser.
Implementationer.
Vi betragter nu flere forskellige implementationer af forén-og-find. Alle er baseret på en række id[] af heltalsværdier, indekseret af elementerne. Således bruger vi værdierne id[p] og id[q] for at afgøre, elementerne \(p\) og \(q\) tilhører samme komponent.- Hurtigt fund.
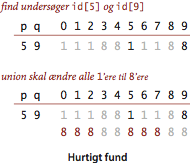
Programmet QuickFindUF.java opretholder
invarianten, at p og q er sammenhængende, hvis og
kun hvis id[p] == id[q].
Med andre ord har alle elementer i samme komponent den samme værdi i
id[].
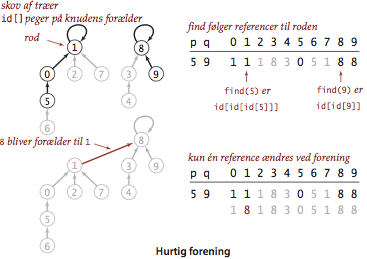
- Hurtig forening.
Programmet QuickUnionUF.java er ligeledes
baseret på en elementindekseret række id[], men bruger en
anden fortolkning af værdierne.
Dette leder til en mere indviklet struktur, hvor elementets indgang i
rækken id[] henviser til et anden element i samme komponent
(muligvis elementet selv).
For at implementere find() begynder vi fra det givne element,
følger dens henvisninger til et andet element, følger dennes
henvisning til yderligere et element, og så videre, indtil vi når
strukturens rod, dvs.
det element, der henviser til sig selv.
Invarianten er, at to elementer tilhører samme komponent, hvis og kun
hvis denne proces leder til samme rod.
Vores implementation union() skal opretholde denne invariant.
Hertil følger vi henvisninger til begge givne elementers rødder, og
omdøber den ene komponent ved at lade en af rødderne henvise til den
anden.
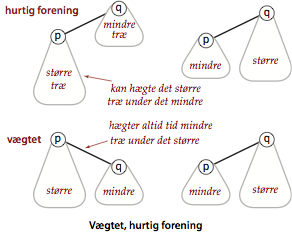
- Vægtet forening.
Vi vil nu forbedre implementationen af union() i algoritmen
for hurtig forening.
I stedet for at vilkårligt hægte det andet træ under det første
holder vi styr på begge træstørrelserne og hægter altid det mindre
træ under det større.
Programmet WeightedQuickUnionUF.java
implementerer denne tilgang.
- Vægtet forening med vejforkortning. Kan vi yderligere forbedre algoritmen for vægtet, hurtig forening? Fund er hurtigst, når hver knude er hægtet direkte til roden i sit træ, men sådan en datastruktur indebærer, at vi skal ændre et stort antal henvisninger ved forening. Vi kan komme tæt på idealet ved at hægte knuder direkte til roden, hver gang vi besøger dem.
Omkostningsmodel for forén-og-find.
For at vurdere algoritmer for forén og find, tæller vi antallet af rækkeadgange, dvs. antallet af læse- og skriveoperationer til indgange i rækken id[].Definitioner.
Størrelsen af et træ er antallet af træets knuder. Dybden af en knude i træet er antallet af henvisninger på vejen fra knuden til træet rod. Træets højde er den største dybde af dets knuder.Påstand.
Hurtigt fund anvender \(1\) rækkeadgang for hvert kald af find() og mellem \(N+3\) og \(2N+1\) rækkeadgange for hvert kald af union(), der forener to komponenter.Påstand.
Antallet af rækkeadgange for et kald af find(p) i hurtig forening er \(1+2d(p)\), hvor \(d(p)\) er dybden af den knude, der svarer til elementet \(p\). Antallet af rækkeadgange for et kald af union() og connected() er omkostningen for de to kald af find() (plus 1 for union() hvis de to givne elementer er i forskellige træer).Påstand.
Dybden af hver knude i skoven konstrueret af vægtet, hurtig forening af \(N\) elementer er højst \(\operatorname{lg} N\).Korollar.
Værstefaldstilvæksten af omkostningen per operation for find(), connected() og union() ved vægtet, hurtig forening af \(N\) elementer er højst \(\operatorname{lg} N\).| Algoritme | konstruktion | forening | fund |
|---|---|---|---|
| hurtigt fund | \(N\) | \(N\) | \(1\) |
| hurtig forening | \(N\) | træhøjde | træhøjde |
| vægtet, hurtig forening | \(N\) | \(\operatorname{lg} N\) | \(\operatorname{lg} N\) |
| vægtet, hurtig forening med vejforkortning | \(N\) | meget tæt på 1 (amortiseret) se opgave 1.5.13 i [SW] | |
| umulig | \(N\) | \(1\) | \(1\) |
