1.4 Algoritmeanalyse
Algoritmeanalyse prøver at finde svar på spørgsmål som
- Hvorfor kører mit program så langsomt?
- Hvorfor løber mit program tør for lagerplads?
Den videnskabelige metode.
Vi kan analysere programmers tidsforbrug med samme metode, som naturvidenskaberne bruger til at forstå verden omkring os:
- Observere en egenskab ved den naturlige verden, gerne ved hjælp af nøjagtige målinger.
- Opstille en hypotese eller model som er konsistent med observationerne.
- Forudsige hændelser med udgangspunkt i hypotesen.
- Verificere forudsigelserne ved hjælp af yderligere observationer.
- Validere ved at gentage processsen indtil hypotesen og observationerne stemmer overens.
Observationer.
Vi begynder med at foretage kvantitative målinger af programmers tidsforbrug. Hertil bruger vi datatypen Stopwatch.java, der måler køretiden af et program.Programmet for tresummer, ThreeSum.java, læser \(N\) heltal og tæller antallet af tripler, der summerer til 0. (Programmet tager ikke hensym til heltalsoverløb.) Testprogrammet DoublingTest.java kalder tresumskoden på indput af voksende størrelse som følger. Testprogrammet skaber en række af \(N\) tilfældige heltal og udskriver tiden for kørslen af ThreeSum.count() på dette indput. Derefter fordobles \(N\) og processen gentages.
public class Stopwatch Stopwatch() skab nyt stopur double elapsedTime() tid siden skabelse (i sekunder)
Matematiske modeller.
Et programs samlede køretid afhænger hovedsageligt af to faktorer: omkostningen af den enkelte sætning og antallet af gange, hver enkelt sætning udføres.
- Tildetilnærmelser.
Vi angive funktioner tilnærmelsesvis ved at bruge tildenotationen.
Dette notation undertrykker lavere ordens termer, som ellers ville
gøre vores formler unødigt komplicerede.
Vi skriver \(\sim f(N)\) for at betegne enhver funktion som efter
division med \(f(N)\) går mod \(1\) som \(N\) vokser.
Vi skriver \(g(N) ~\sim f(N)\) for at angive at \(g(N) / f(N)\) går
mod \(1\) som \(N\) vokser.
funktion tildetilnærmelse vækstrate \(\frac{1}{6}N^3– \frac{1}{2}N^2 + \frac{1}{3}N\) \(\sim \frac{1}{6}N^3 \) \(N^3\) \(\frac{1}{2}N^2 – \frac{1}{2}N\) \(\sim \frac{1}{2}N^2\) \(N^2\) \(\operatorname{lg} N + 1\) \(\sim\operatorname{lg} N\) \(\operatorname{lg} N\) \(3\) \(3\) \(1\) - Klassifikation af funktioners vækstrater.
Vores algoritmeimplementationer bruger ganske få strukturelle
primitiver: sætninger, betingelser, løkker, indre løkker og
funktionskald.
Derfor støder vi ofte på de samme funktioner igen og igen, når vi
angiver omkostningens vækstrate som funktion af problemstørrelsen
\(N\).
De fleste af vores funktioner er på formen \(g(N) \sim a f(N)\), hvor
\(f(N) = N^b \log^c N\), for nogle konstanter \(a\), \(b\) og \(c\).
Vi kalder \(f(N)\) for vækstraten af \(g(N)\), og vi siger at
\(f(N)\) er proportional med \(g(N)\).
navn vækstrate typisk kodestump beskrivelse eksempel konstant \(1\) a = b + c
sætning læg to tal sammen logaritmisk \(\operatorname{lg} N\) se [SW, s. 47] halvering binær søgning lineær N double max = a[0]; for (int i = 1; i < N; ++i) if (a[i] < max) max = a[i];løkke find rækkemaksimum linearitmisk \(N\operatorname{lg} N\) se [SW, algoritme 2.4] del og hersk flettesortering kvadratisk \(N^2\) for (int i = 0; i < N; ++i) for (int j = i+1; j < N; ++j) if (a[i] + a[j] == 0) ++cnt;dobbelt løkke betragt alle par kubisk \(N^3\) for (int i = 0; i < N; ++i) for (int j = i+1; j < N; ++j) for (int k = j+1; j < N; ++k) if (a[i] + a[j] + a[k] == 0) ++cnt;tredobbelt løkke betragt alle tripler eksponentiel \(2^N\) se [SW, kapitel 6] udtømmende søgning betragt alle delmængder Klassifikation af vækstrater - Omkostningsmodel. For hver algoritme formulerer vi en omkostningsmodel der definerer algoritmens grundlæggende operationer. For eksempel er en passende omkostningsmodel for tresumsproblemet antallet af rækkeadgange, dvs. antallet læsninger eller skrivninger til rækken.
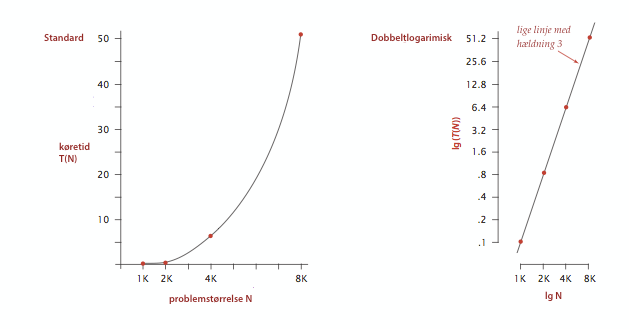
Egenskab. Vækstraten for køretiden af ThreeSum.java er \(N^3\).
Påstand. Den naive algoritme for tresum bruger \(\sim \frac{1}{2}N^3\) rækkeadgange for blandt \(N\) tal at finde antallet af tripler der summer til \(0\).
Konstruktion af hurtigere algoritmer.
Hovedanledningen for at studere vækstraten af programmers køretid er som hjælp til at konstruere hurtigere algoritmer for at løse det samme problem. Vi kan fx udvikle hurtigere algoritmer for tosums- og tresumsproblemerne ved at bruge flettesortering og binærsøgning.- Tosum. Udtømmende søgning som i programmet TwoSum.java tager tid proportional med \(N^2\). Programmet TwoSumFast.java løser tosumsproblemet i tid proportional med \(N\log N\).
- Tresum. Programmet ThreeSumFast.java løser tresumsproblemet i tid proportional med \(N^2\log N\).
Afhængighed af indput.
Det viser sig, at mange af vores algoritmer har køretider som vi kan karakterisere som funktion af størrelsen af indput. Der findes dog situationer, hvor denne meget enkle model ikke er tilstrækkelig.- Indputmodeller. Vi kan prøve at opstille mere præcise modeller for inputs beskaffenhed. Denne tilgang er dog behæftet med vanskeligheder. Dels kan modellen kan være urealistisk, fx når man antager, at indput er uniformt fordelt tilfældig. Dels kan det være overordentligt vanskeligt at matematisk gennemføre den slags analyser.
- Værstefaldsgarantier. Et programs værstefaldskøretid gælder uanset inputs beskaffenhed, dvs. at den beskriver opførslen for den værst tænkelige situation. Denne konservative tilgang er passende for programmer som styrer et kernekraftværk, en pacemaker eller bremsesystemet i en bil.
- Randomiserede algoritmer. Mange hurtige algoritmer bruger tilfældighed eller randomisering, fx kviksortering og spredetabeller. Køretiden er nu ikke længere kun afhængig af indput, men kan ændre sig, hver gang algoritmen køres. For at analysere den slags algoritmer bruges sandsynlighedsteori til at give køretidsgarantier, der gælder med overvældende sandsynlighed. I praksis er disse garantier ofte lige så gode som værstefaldsgarantierne; sandsynligheden for at de fejler er mindre end sandsyndligheden for at computeren bliver ramt af lynet under kørslen.
- Amortiseret analyse. I mange anvendelser er vi mest interesseret i, hvordan en algoritme eller datastruktur håndterer en hel sekvens af operationer. Amortiseret analyse er en teknik til at give værstefaldsgarantier på en sådan sekvens af operationer.
Påstand. Iimplementationen af sæk, stak og kø som en hægtet liste tager alle operationer konstant tid i værste fald.
Påstand. I implementationen af sæk, stak og kø som en dynamisk række tager alle operationer amortiseret konstant tid per operation i værste fald. Med andre ord tager hver sekvens af \(N\) operationer, begyndende med en tom datastruktur, tid proportionalt med \(N\) i værste fald.
Lagerforbrug.
For at afgøre, hvor meget lager vores program bruger, tæller vi antallet af variaber og vægter dem efter, hvor mange bytes deres datatype bruger. For en typisk 64-bitsmaskine har vi:
- Primitive typer.
Følgende tabel angiver lagerforbruget for de primitive typer:
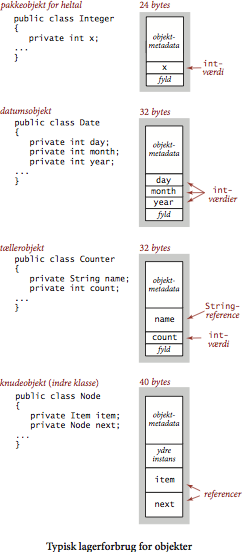
type lagerforbrug (bytes) boolean 1 byte 1 char 2 int 4 float 4 long 8 double 8 - Objekter. Lagerforbruget for et objekt er givet ved lagerforbruget af hver instansvariabel. Hertil kommer et merforbrug på typisk 16 byte for metadata, som bruges til at administrere objektet. Her ligger fx en henvisning til objektets klasse samt information som bruges til lagerspildshåndtering. På en typisk 64-bitsmaskine rundes dette desuden op til nærmeste multiplum af 8 byte.
- Referencer. En objektreference består typisk af en lageradresse og bruger defor 8 byte lager på en 64-bitsmaskine.
- Hægtede lister. Hvert element i en hægtet liste repræsenteres af knudeklassen Node, som tager 16 byte for metadata, 8 byte for instansvariabeln next. 8 byte for instansvariabel item. En ikke-statisk, indre klasse som Node kræver yderligere 8 byte til at gemme henvisningen til den omsluttende instans. Hele knudeobjektet fylder altså 40 byte. Vi kan beregne lagerforbruget for en stak af \(N\) heltal implementeret som hægtet liste. Et objekt fra referenceklassen for heltal Integer tager 24 byte, hver knude tager 40 byte. Hertil kommer 32 for stakken: 16 byte metadata for objektet, 8 byte for referencen til staktoppen first, 4 byte for heltalsvariabeln N og 4 byte fyld. Sammenlagt bruger hele stakken \(32+64N\) byte.
- Rækker.
Javas rækker er implementeret som objekter, og gemmer desuden
rækkens længde.
En række af primitive værdier tager fx 24 byte: 16 byte metadata til
objektadministration, 4 byte for længden og 4 byte fyld for at runde
af til et multiplum af 8 byte.
Hertil kommer så pladsen for at lagre selve værdierne; en række af
\(N\) heltal af referencetypen Integer bruger altså
sammenlagt \(24+(8+24)N = 24 +32N\) byte.
type lagerforbrug (byte) int[N] \(\sim 4N\) double[N] \(\sim 8N\) Date[N] \(\sim 40N\) double[N][M] \(\sim 8NM\) - Strenge.
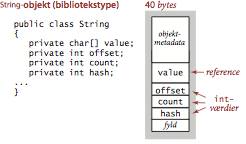
En streng af længde \(N\) bruger 40 byte til objektet String
plus \(24 + 2N\) byte for rækken med de enkelte tegn af typen
char.
Sammenlagt bruger strengen \(64 + 2N\) byte.