4.2 Rettede grafer
Rettede grafer.
En rettet graf består af en mængde af knuder og en samling af rettede kanter, der hver forbinder et par af knuder \((u,v)\). Vi siger, at den rettede kant peger fra parrets første knude \(u\) og peger på parrets anden knude \(v\). Vi bruger tallene \(\{0,\ldots V-1\}\) for at navngive knuderne i en graf med \(V\) knuder.
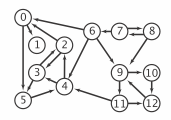
Glosar.
Vi benytter følgende definitioner og terminologi.- En løkke er en kant, der peger fra en knude til sig selv.
- To kanter er parallelle, hvis de forbinder det samme ordnede par af knuder.
- En knudes udgrad er antallet af kanter, der peger fra den. En knudes indgrad er antallet af kanter, der peger på den.
- En delgraf en en delmængde af grafens rettede kanter samt deres endeknuder.
- En rettet sti i en rettet graf er en sekvens af knuder, hvor der er en (rettet) kant fra hver knude til knudens efterfølger i sekvensen. En simpel sti er en sti uden gentagne knuder.
- En rettet kreds er en rettet sti med mindst en kant, hvor stiens første og sidste knude er den samme. En simpel, rettet kreds er en rettet kreds uden gentagne knuder, bortset fra stiens første og sidste knude.
- Længden af en sti eller kreds er antallet af kanter.
- Knuden \(w\) kan nås fra eller er tilgænglig fra knuden \(v\) hvis der er en rettet sti fra \(v\) til \(w\).
- To knuder \(v\) og \(w\) kaldes stærkt sammenhængende hvis de kan nås fra hinanden, dvs. hvis der er en rettet sti fra \(v\) til \(w\) og en rettet sti fra \(w\) til \(v\).
- En rettet graf er stærkt sammenhængende hvis der findes en rettet sti fra hver knude til hver anden knude.
- En rettet graf som ikke er stærkt sammenhængende, består af mindst to stærke sammenhængskomponenter, som udgøres af grafens maksimale, stærkt sammenhængende delgrafer.
- En rettet acyklisk graf (RAG) er en rettet graf som ikke indeholder nogen rettet kreds.
- Omvendingen \(G^R\) af den rettede graf \(G\) opstår ved at bytte retning på hver kant i \(G\).
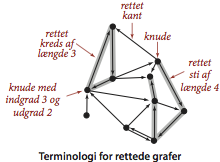
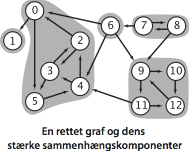
Datatype for rettede grafer.
Vi implementerer følgende APG for rettede grafer.
| public class Digraph | ||
|---|---|---|
| Digraph(int V) | rettet graf med \(V\) knuder og ingen kanter | |
| Graph(In in) | rettet graf fra indputstrømmen in | |
| int | V() | antal knuder |
| int | E() | antal kanter |
| void | addEdge(int v, int w) | tilføj kanten v->w til denne graf |
| Iterable<Integer> | adj(int v) | naboknuder som kanter fra \(v\) peger på |
| Digraph | reverse() | grafens omvending |
| String | toString() | tekstuel repræsentation af grafen |
Den centrale metode er nabogennemløberen adj(), som tillader klientkoden at gennemløbe alle naboer, som den givne knudes nabokanter peger på.
Vores testdata tinyDG.txt og tinyDAG.txt bruger følgende indputformat:
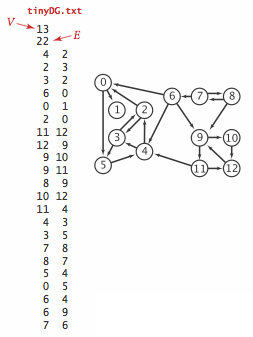
Grafrepræsentation.
Vi repræsenterer grafer som nabolister. Det vil sige, at vi opretholder en knude-indekseret række af lister, som for hver knude indeholder de knuder, som knudens nabokanter peger på.
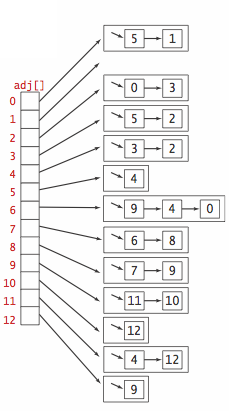
Programmet Digraph.java implementer APG’en for rettede grafer ved brug af nabolisterepræsentationen. Til sammenligning implementerer programmet AdjMatrixDigraph.java samme APG ved brug af nabomatrixrepræsentationen; her repræsenteres grafen af en boolsk matrix \(A\), hvis indgang \(A_{uv\}\) beskriver, om der findes en kant fra \(u\) til \(v\).
Tilgængelighed i rettede grafer.
Både dybde-først- og bredde-først-søgning virker for rettede grafer.- Tilgængelighed fra en enkelt kilde: Givet en rettet graf med startknude \(s\), er der en rettet sti fra \(s\) til \(v\)? Find i givet fald en sådan sti. Programmet DirectedDFS.java løser dette problem med dybde-først-søgning.
- Tilgængelighed fra flere kilder: Givet en rettet graf og en mængde af startknuder, er der en rettet sti fra nogen startknude til \(v\)? Programmet DirectedDFS.java løser dette problem med dybde-først-søgning.
- Rettede stier fra en enkelt kilde: Givet en rettet graf og en startknude s, byg en datastruktur der støtter spørgsmål af slagsen «Er der den rettet sti fra \(s\) til \(v\)?» og i givet fald finder en sådan sti. Programmet DepthFirstDirectedPaths.java løser dette problem med dybde-først-søgning.
- Korteste rettede stier fra en enkelt kilde: Givet en rettet graf og en startknude \(s\), byg en datastruktur der støtter spørgsmål af slagsen «Er der den rettet sti fra \(s\) til \(v\)?» og i givet fald finder en sådan korteste sti fra \(s\) til \(v\). BreadthFristDirectedPaths.java løser dette problem med bredde-først-søgning.
Kredse og rettede acykliske grafer.
Rettede kredse spiller en vigtig rolle for anvendelser, der behandler rettede grafer.
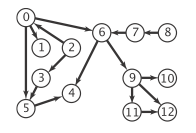
- Finde rettede kredse: Indeholder en givet rettet graf
en rettet kreds?
Find i given fald en sådan kreds.
Programmet DirectedCycle.java løser dette
problem med dybde-først-søgning.
- Dybde-først-orden: Dybde-først-søgning besøger hver
knude præcis en gang.
Følgende knudeordninger forekommer i typiske anvendelser.
- Præorden: Stil knuden i kø før de rekursive kald.
- Postorden: Stil knuden i kø efter de rekursive kald.
- Omvendt postorden: Læg knuden på stakken efter det rekursive kald.
Programmet DepthFirstOrder.java beregner disse ordener.

- Topologisk sortering: Givet en rettet graf, ordn
knuderne således at alle rettede kanter peger fra en lavere ordens
knude til en højere ordens knude (eller afgør at en sådan ordning
ikke findes.)
Programmet Topological.java løser dette
problem med dybde-først-søgning.
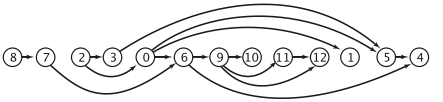
Påstand.
En rettet graf har en topologisk orden hvis og kun hvis den er acyklisk.Påstand.
Omvendt postorden i en rettet acyklisk graf er en topologisk orden.Påstand.
Dybde-først-søgning finder en topologisk orden i en rettet, acyklisk graf i tid proportional med \( V+ E\).Stærk sammenhæng.
Stærk sammenhæng er en ækvivalensrelation på mængden af knuder:- Refleksivitet: Hver knude \(v\) er stærkt sammenhængende med sig selv.
- Symmetri: Hvis \(v\) er stærk sammenhængende med \(w\), så er \(w\) stærkt sammenhængende med \(v\).
- Transitivitet: Hvis \(v\) er stærk sammenhængende med \(w\), og \(w\) er stærk sammenhængende med \(x\), så er \(v\) stærkt sammenhængende med \(x\).
| public class SCC | ||
|---|---|---|
| SCC(Digraph G) | forbehandl grafen | |
| boolean | stronglyConnected(int v, int w) | er u og v stærkt sammenhængende |
| int | count() | antal stærke sammenhængskomponenter |
| int | id(int v) | komponentnavn for knuden v (mellem 0 og count()-1) |
Kosaraju og Sharirs forbløffende algoritme i programmet KosarajuSharirSCC.java implementerer denne APG med blot nogle få ekstra linjer kode ud over CC.java. Idéen er følgende:
- Givet en rettet graf \(G\), konstruér dens omvending \(G^R\) og brug dybde-først-gennemløbet fra DepthFirstOrder.java for at beregne en omvendt postorden af \(G^R\).
- Udfør et almindeligt dybde-først-gennemløb på \(G\), men betragt de umarkerede knuder i den netop beregnede omvendte postorden af \(G^R\).
- Alle knuder, som nås ved det rekursive kald af dfs() fra konstruktøren tilhører samme stærke sammenhængskomponent(!), og får derfor samme komponent-id.
Påstand.
Kosaraju og Sharirs algoritme bruger forbehandlingstid og -plads proportional med \( V + E\) for at besvare sammenhængsforespørgsler i en rettet graf i konstant tid.Transitiv afslutning.
Den transitive afslutning \(T(G)\) af en rettet graf \( G\) er en rettet graf med samme knudemængde. Der er en kant fra \(u\) til \(v\) i \(T(G)\) hvis og kun hvis der er en sti fra \(u\) til \(v\) i \(G\).
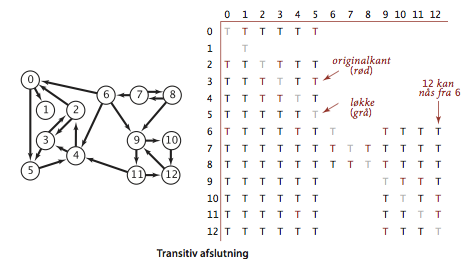
Programmet TransitiveClosure.java
beregner den transitive afslutning af en rettet graf ved at
dybde-først-søge fra hver knude.
Denne løsning er ideel for små og tætte grafer.
Løsningen er ikke god for store, tynde grafer, fordi konstruktøren
bruger plads proportional med \( V^2 \) og tid proportional med \(V(
V+E)\).
