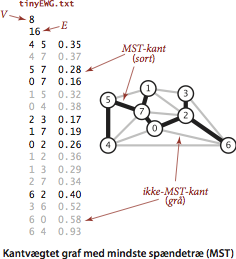
4.3 Mindste spændetræ
Mindste spændetræ.
Et spændegraf af en graf er en delgraf, som indeholder alle grafens knuder. Et spændetræ af en sammenhængende graf er en acyklisk spændegraf. En kantvægtet graf er en graf, hvor der er knyttet en vægt eller omkostning til hver kant. Et mindste spændetræ (MST) (eller letteste spændetræ) af en kantvægtet graf er et spændetræ, hvis totale vægt (dvs. summen af kantvægtene) ikke er større end vægten af noget andet spændetræ.
Antagelser.
Vi vedtager følgende konventioner:- Grafen er sammenhængende. Definitionen af spændetræ kræver, at grafen er sammenhængende. Hvis grafen er usammenhængende, kan vi ændre vores algoritmer til at beregne et mindste spændetræ for hver sammenhængskomponent. Foreningen af disse træer kaldes en mindste spændeskov.
- Kantvægte er ikke nødvendigvis afstande. Selvom geometrisk intuition ofte er en fordel, kan kantvægtene være vilkårlig og behøver fx ikke at opfylde trekantsuligheden.
- Kantvægt kan være nul eller negativ. Hvis alle kantvægte er positive, kan vi definere MST som en mindste spændegraf, dvs. at vi ikke behøver at gøre kravet om acyklicitet eksplicit. (Det indses dog, at en mindste spændegraf må være et træ.)
- Alle kantvægte er forskellige. Hvis kanter kan have samme vægt, er det mindste spændetræ ikke nødvendigvis entydigt bestemt. Ved at antage unikke kantvægte bliver nogle af vores beviser en smule enklere. Det skal dog understreges, at alle vores algoritmer stadig fungerer korrekt, hvis grafen har gentagne kantvægte.
Grundlæggende principper.
Vi minder om to de afgørende egenskaber ved et træ:- Tilføjelse af en kant mellem to knuder i et træ skaber en unik kreds.
- Fjernelse af en kant fra et træ bryder det i to separate undertræer.

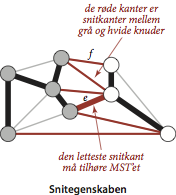
Et snit i en graf er en opdeling af knudemængden i to
disjunkte mængder.
En snitkant i et snit er en kant, hvis endepunkter
ligger på hver sin side af snittet.
Påstand. (Snitegenskaben)
Betragt et snit i en kantvægtet graf, hvis kantvægte er forskellige. Den snitkant, som har mindst vægt, tilhører grafens mindste spændetræ.
Snitegenskaben er gundlaget for vores MST-algoritmer.
De er eksempler på en generel problemløsningsteknik, som hedder
grådige algoritmer .
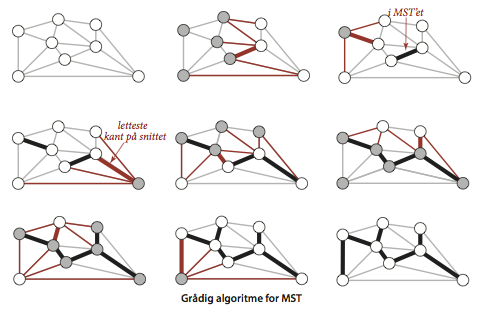
Påstand. (Grådig algoritme for MST)
Følgende fremgangsmåde farver alle kanter i et MST i en sammenhængende kantvægtet graf med \(V\) knuder med sort:- Begynd med alle kanter farvet gråt.
- Find et snit uden sorte snitkanter.
- Farv den lettest snitkant sort.
- Fortsæt indtil \(V–1\) kanter er sorte.
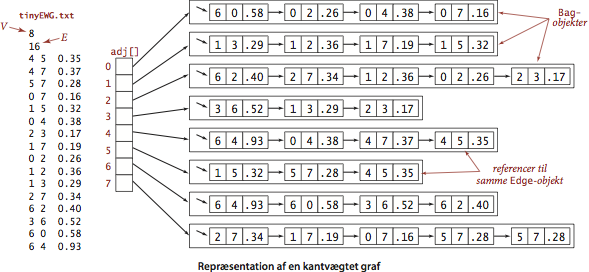
Datatype for kantvægtede grafer.
Vi repræsenterer vægtede kanter med følgende APG:
| public class Edge implements Comparable<Edge> | ||
|---|---|---|
| Edge(int v, int w, double weight) | skab en kant mellem v og w med vægt weight | |
| double | weight() | denne kants vægt |
| int | either() | en af kantens endeknuder |
| void | other(int v) | den anden endeknude |
| int | compareTo(Edge that) | sammenlign denne kant med kanten that |
| String | toString() | tekstuel repræsentation af kanten |
Vi repræsenterer kantvægtede grafer med af følgende APG:
| public class EdgeWeightedGraph | ||
|---|---|---|
| Graph(int V) | skab en graf med V knuder og ingen kanter | |
| Graph(In in) | læs en graf fra indputstrømmen in | |
| int | V() | antal knuder |
| int | E() | antal kanter |
| void | addEdge(Edge e) | tilføj kanten e til denne graf |
| Iterable<Edge> | adj(int v) | nabokanter til v |
| Iterable<Edge> | edges() | alle kanter i denne graf |
| String | toString() | tekstuel repræsentation af grafen |
APG for MST.
Vi bruger følgende APG til beregning af et MST af en kantvægtet graf:
| public class MST | ||
|---|---|---|
| MST(EdgeWeightedGraph G) | konstruktør | |
| Iterable<Edge> | edges() | alle kanter i MST |
| double | weight() | MST’s samlede vægt |
- tinyEWG.txt indeholder 8 knuder og 16 kanter
- mediumEWG.txt indeholder 250 knuder og 1.273 kanter
- 1000EWG.txt indeholder 1.000 toppunkter og 8,433 kanter
- 10000EWG.txt indeholder 10.000 knuder og 61,731 kanter
- largeEWG.txt indeholder en million knuder og 7,586,063 kanter
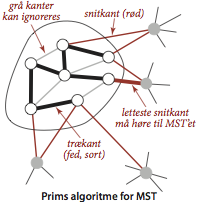
Prims algoritme.
Prims algoritme udvider et træ med en kant ad gangen. Begynd med en enkel knude som træets eneste knude. Tilføj derefter \(V-1\) kanter til træet, ved gentagne gange at tage den letteste kant blandt de kanter, der forbinder en knude i træet med en knude uden for træet. (Med andre ord defineres snittet af de knuder, der tilhører træet.)
Beskrivelsen af Prim algoritme foroven i en enkelt sætning lader det
centrale spørgsmål ubesvaret:
Hvordan kan vi (effektivt) finde den letteste snitkant?
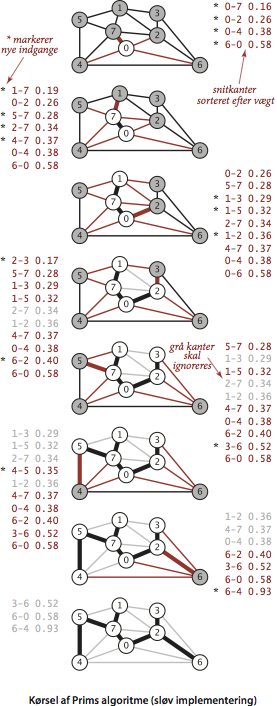
- Sløv implementering.
Vi bruger en prioritetskø til at holde styr på snitkanterne og
finde den letteste.
Vi udvider træet med denne letteste snitkant og den nye knude,
kanten fører til.
Denne knudes nabokanter gennemgås, og snitkanterne stilles i
prioritetskøen.
Dette gentages til træet indeholder \(V-1\) kanter.
Bemærk, at kanter i prioritetskøen undervejs kan holde op med at være
snitkanter, fordi deres andet endepunkt blev indsat i træet via en
anden kant.
Den sløve implementation lader disse kanter forblive i
prioritetskøen til de afkøs;
på det tidspunkt er det nemt at se, om de skal ignoreres, fordi de
har begge endepunkter i træet.
Programmet LazyPrimMST.java implementerer den sløve fremgangsmåde. Prioritetskøen er fra programmet MinPQ.java.
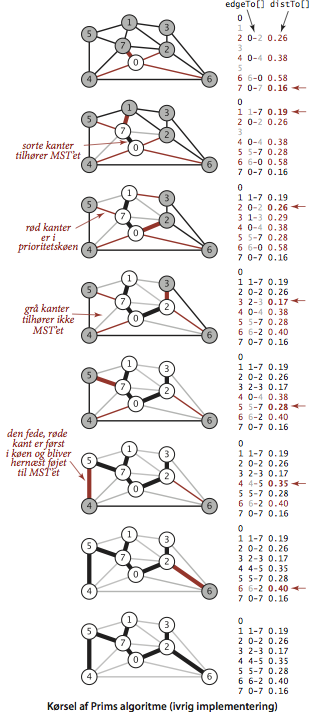
- Ivrig implementering.
For at forbedre den sløve implementation af Prims algoritme
opretholder vi som invariant, at prioritetskøen kun består af
snitkanter.
Faktisk kan vi fjerne endnu flere kanter.
Bemærk nemlig, at vi kun interesser os for den letteste
kant mellem nogen træknude og nogen ikke-træknude.
Antag at vi tilføjer en knude \(v\) til træet.
Set fra en ikke-træknude \(w\) er den eneste ændring ved
tilføjelsen af \(v\), at \( w\) er blevet bragt »tættere« til
træet.
Vi har altså ikke brug for at holde alle nabokanter til
\(w\) i køen; vi kan nøjes med at holde styr på den letteste
nabokant og skal så blot kontrollere, om tilføjelsen af knuden
\(v\) til træet nødvendiggør, at vi opdaterer dette minimum.
Dette sker når kanten \(vw\) har lavere vægt, hvilket vi kan
undersøge når vi behandler kanterne hørende til \(v\).
Med andre ord er invarianten, at prioritetskøen indeholder den
letteste snitkant hørende til hver ikke-træknude.
Programmet PrimMST.java er en implementation af den ivrige fremgangsmåde. Den bruger en indekseret prioritetskø fra IndexMinPQ.java .
Påstand.
Prims algoritme beregner MST af en sammenhængende, kantvægtet graf. Den sløve version af Prims algoritme bruger plads proportional med \(E\) og værstefaldstid proportional med \(E \log E\) for at beregne MST af en sammenhængende kantvægtet graf med \(E\) kanter og \(V\) knuder. Den ivrige versionen af Prims algoritme bruger plads proportional med \(V\) og værstefaldstid proportional med \(E\log V\).
Kruskals algoritme.
Kruskals algoritme behandler samtlige kanter i rækkefølge efter deres vægt, fra lettest til tungest. Hver kant farves sort, hvis den ikke danner en kreds med de andre sorte kanter. Denne proces standser efter at \(V–1\) kanter er farvet sort, som nu danner et minste spændetræ. De sorte kanter danner altså undervejs en skov af træer, der gradvist vokser sammen til et en enkelt træ.
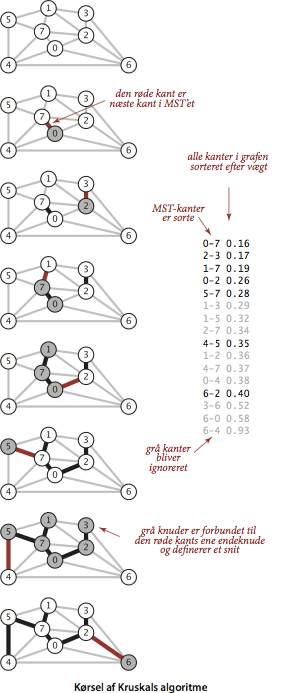
For at implementere Kruskals algoritme bruger vi en prioritetskø til
at behandle kanterne i rækkefølge efter vægt, en forén og
find-datastrukturen til at identificere kredse og en kø til at
indsamle MST-kanter.
Programmet KruskalMST.java
implementerer Kruskals algoritme på den måde.
DPrioritetskøen er fra MinPQ.java
, sammenhængskomponenterne fra UF.java
, og køen fra Queue.java .
