2.4 Prioritetskøer
Vi betragter nu yderligere samlingstype, prioritetskøen, som kan opfattes som en mere fleskibel struktur end stakken og køen. Elementerne i en prioritetskø skal være sammenlignelige, dvs. at det giver mening at tale om et “største” element i køen. Prioritetskøen understøtter to operationer: fjernelse af maksimum og indsættelse. Til sammenligning fjerner køen det først indsatte element, stakken fjerner det sidst indsatte element og prioritetskøen fjerner et største element, uanset hvornår det blev sat ind.
Programmeringsgrænseflade.
Vores konvention er at sammenligne nøgler udelukkende med metoden less(), ganske som vi gjorde for sortering. Hvis der altså er flere poster med samme maksimale nøgle, henviser maksimum til en vilkårlig blandt disse poster med størst nøgler. Programmeringsgrænsefladen afrundes med konstruktører og en metode til at afgøre, om køen er tom. For fleksibilitetens skyld implementerer vi datastrukturen for en generiske nøgletype Key som implementerer sammenlignergrænsefladen Comparable.
public class MaxPQ<Key extends Comparable<Key>> MaxPQ() en tom prioritetskø MaxPQ(int max) en tom prioritetskø med initialkapacitet max MaxPQ(Key[] a) en prioritetskø af nøglerne i a[] void insert(Key v) indsæt en nøgle Key max() returnér en største nøgle Key delMax() returnér og fjern en største nøgle boolean isEmpty() er prioritetskøen tom? int size() antal elementer i prioritetskøen
Programmet TopM.java er en prioritetskøklient, som fra standardindput læser et heltal M og en følge transaktioner og skriver de M største transaktioner.
Grundlæggende implementationer.
De grundlæggende datastrukturer fra kapitel 2 giver os fire umiddelare udgangspunkter for implementationen af prioritetskøer.- Usorteret række. Den måske enkleste prioritetskøimplementation baserer sig på vores kode for stakke. Koden for indsættelse i prioritetskøen bliver den samme som for at lægge et element på stakken. For at fjerne maksimum bruger vi samme ide som for den indre løkke i udvalgssortering: Find maksimum ved lineært gennemløb og lad det bytte plads med rækkens sidste element, hvorefter det kan fjernes ligesom ved afstakning. Programmet UnorderedArrayMaxPQ.java implementerer en prioritetskø med denne ide.
- Sorteret række. En anden tilgang er at udvide koden for indsættelse til at flytte større elementer en position til højre, hvorved hele rækken beholdes i sorteret orden, ligesom ved indsættelsessortering. Hermed er rækkens sidste element altid et største element, og koden for fjernelse af maksimum i prioritetskøen er identisk med afstakning. Programmet OrderedArrayMaxPQ.java implementerer en prioritetskø med denne ide.
- Hægtede lister. I stedet for rækker kan vi også bruge vores stakimplementation med hægtet liste. Enten skal vi ændre koden for afstakningmetoden pop(), så den finder, flytter og returnerer maksimum i en usorteret liste. Ellers skal vi ændre koden for indsættelsesmetoden push() så den holder alle elementer i omvendt sorteret orden.
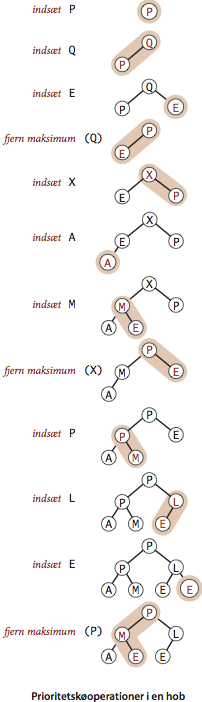
operation argument returværdi størrelse indhold (ej sorteret) indhold (sorteret) indsæt P 1 P P indsæt Q 2 P Q P Q indsæt E 3 P Q E E P Q fjern maksimum Q 2 P E E P indsæt X 3 P E X E P X indsæt A 4 P E X A A E P X indsæt M 5 P E X A M A E M P X fjern maksimum X 4 P E M A A E M P indsæt P 5 P E M A P A E M P P indsæt L 6 P E M A P L A E L M P P indsæt E 7 P E M A P L E A E E L M P P fjern maksimum P 6 E E M A P L A E E L M
De grundlæggende implementationer foroven har alle den egenskab, at værstefaldskøretiden for enten indsættelse eller fjernelse af maksimum er lineær. Vi skal nu betragte en implementation hvor begge operationer er garanteret hurtige.
Hobe.
En binærhob er en datastruktur, som understøtter priotetskøoperationerne på en effektiv måde. I en binærhob er elementerne gemt i en række, sådan at hver nøgle er større end eller lig med nøglerne på to andre, specifikke positioner, som vi skal bestemme nærmere forneden. Hver af disse nøgler er igen mindste lige så stor som to andre nøgler, og så videre. Denne ordning er nemt at visualisere, når vi betragter nøglerne i et binærtræ, hvor en nøgles to børn er de to nøgler, der skal være mindre.Definition (hobinvariant). Et binærtræ af nøgler er hobordnet, hvis hver knudes nøgle er større end eller lig med dens børns nøgler.
Påstand. Roden i et hobordnet binærtræ indeholder en største nøgle.
Det giver mening at definere hobordning for vilkårlige, rodfæstede træer. Men vi vil først og fremmest betragte fuldstændige binærtræer.
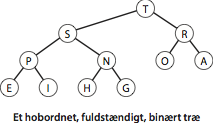
Definition. En binærhob er en mængde af knuder med nøgler, der er anbragt i et fuldstændigt, hobordnet binærtræ, repræsenteret lag for lag i en række. (Rækkens første plads er uanvendt).
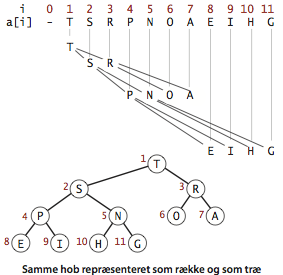
Ifølge vores konventioner ligger forælderen for en knude på plads \(k\) i en hob på plads \(k/2\). Knudens to børn ligger på pladserne \(2k\) og \(2k + 1\). Vi kan altså navigere op og ned ved enkle beregninger på rækkeindices: For at gå opad i træet fra a[k] sætter vi \(k\) til \(k/2\); for at gå nedad i træet sætter vi \(k\) til \(2k\) eller \(2k+1\).
Algoritmer på hobe.
Vi repræsenterer en hob af størrelse N som privat række pq[] af længde N+1 med pq[0] uanvendt og hobens elementer i pq[1] til pq[N]. Vi tilgår nøgler udelukkende ved brug af den private metode less() for at sammenligne og den private metode exch() for at bytte plads. Vores hoboperationer begynder alle med en enkel forandring af hoben, som muligvis forstyrrer hobordningen. Derefter genoprettes ordningen ved at navigere opad eller nedad i hoben og retablere hobinvarianten overalt. Vi kalder denne proces at genoprette hobordningen.- Svømning. Vi kan
genoprette hobordningen nedefra og op ved at lade en konflikt
svømme opad i hoben.
Når hobordningen forstyrres af at en knudes nølge er større end
forælderknudens nøgle, kan vi flytte problemet opad ved at lade knuden
og forælderen bytte plads.
Efter dette bytte er knuden større end begge dens børn: det ene barn
er den gamle forælder (som jo var mindre), den anden var den gamle
forælders barn, som jo (ifølge hobinvarianten) ikke var større end den
gamle forælder.
Givetvis kan knuden stadig være større end sin (nye) forælder, men i
så fald gentages processen bare.
Før eller siden når processen en knude med større nøgle eller selve
roden.
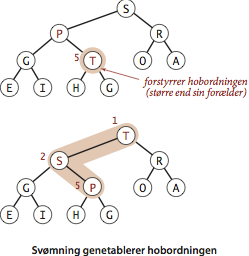
private void swim(int k) { while (k > 1 && less(k/2, k)) { exch(k, k/2); k = k/2; } }
- Synk.
Vi kan genoprette hobordningen oppefra og ned ved at lade en
konflikt synke længere og længere ned i hoben.
Når hobordningen forstyrres af at en knudes nølge er mindre end én
eller begge af dens børneknuders nølger, kan vi flytte problemet
nedad ved at lade knuden bytte plads med den største af børnene.
Dette bytte kan introducere en ny forstyrrelse på barnets plads, i
hvilket fald processen gentages. Før eller siden når processen en
knude, hvis børneknuder begge er mindre, eller hobens bund.
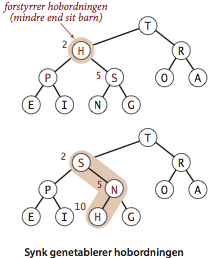
private void sink(int k) { while (2*k <= N) { int j = 2*k; if (j < N && less(j, j+1)) j++; if (!less(k, j)) break; exch(k, j); k = j; } }
Hobbaseret prioritetskø.
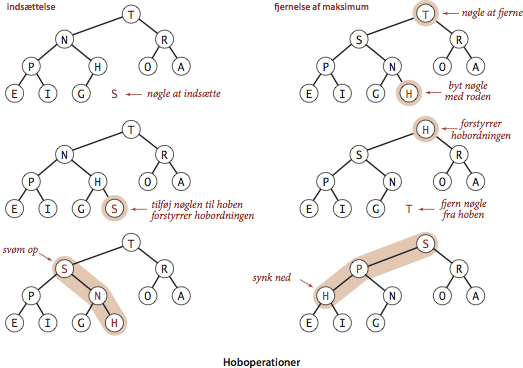
Synk- og svømmeoperationerne sink() og swim() udgør grundlaget for en effektiv implementation af grænsefladen for prioritetskøer. Dette er vist forneden og implementeret i MaxPQ.java og MinPQ.java for fjernelse af henholdsvis maksimum og minimum.- Indsættelse. Det nye element lægges på rækkens sidste plads, hobens størrelse øges med én, og det nye element svømmer på plads for at genoprette hobordningen.
- Fjernelse af maksimum. Elementet ved hobens rod fjernes og erstattes med hobens sidste element. Hobens størrelse mindskes med én. Elementet ved roden synker på plads for at genoprette hobordningen.
Påstand.
I en prioritetskø med N elementer udfører hobalgoritmen højst
1 + lg N sammenligninger for indsættelse og højst 2 lg
N sammenligninger for fjernelse af maksimum.
Praktiske overvejelser.
Vi afslutter vores studie af hobbaserede prioritetskøer med nogle praktiske overvejelser.- Flervejshobe. Det ligger ligefor at modificere koden til at behandle hobe, der er rækkerepræsentationer af fuldstændige, hobordnede ternære eller d-ære træer. Denne idé gør operationerne hurtigere, fordi træhøjden reduceres. Men på den anden side skal man nu finde den største af tre eller d børn.
- Dynamiske rækker. Vi kan tilføje en argumentløs konstruktør, koden for rækkefordobling til indsættelsesmetoden insert() og koden for rækkehalvering i fjernelsesmetoden delMax(), ganske som vi gjorde for stakke i sektion 1.3. Derved bliver de logaritmiske køretider amortiserede.
- Uforanderlige nøgler. Prioritetskøer håndterer objekter, der er blevet skabt af klienter. Vi kræver, at klienterne ikke ændrer disse objekters nøgler, idet sådanne ændringer kunne forstyrre hobinvarianten.
- Indiceret prioritetskø.
I mange anvendelser har klienten brug for at kunne referere til
prioritetskøens elementer.
Hertil knytter vi et unikt heltalsindeks til hvert element.
public class IndexMinPQ<Item extends Comparable<Item>> IndexMinPQ(int maxN) skab en tom prioritetskø med initialkapacitet maxN og mulige indices mellem 0 og maxN-1 void insert(int k, Item item) indsæt elementet item med index k void change(int k, Item item) giv index k til elementet item boolean contains(int k) findes der et element med index k i prioritetskøen? void delete(int k) fjern index k samt elementet indiceret at k Item min() returner et mindste element int minIndex() returner et mindste elements indeks int delMin() fjern et mindste element og returner dets indeks boolean isEmpty() er prioritetskøen tom? int size() antal elementer i prioritetskøen Programmet IndexMinPQ.java er en hobbaseret implmentation af denne programmeringsgrænseflade. Klienten Multiway.java fletter flere sorterede indputstrømme sammen til én strøm.
Hobsortering.
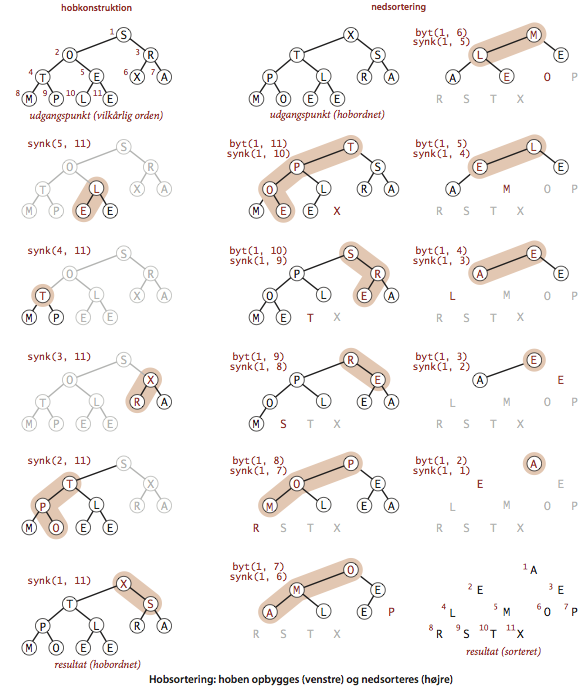
Enhver prioritetskør kan bruges som udgangspunkt for en sorteringsmetode. Vi indsætter alle nøgler i en prioritetskø, hvorefter vi udtager dem i sorteret orden ved at fjerne minimumsnølgen indtil køen er tom. Denne metode kaldes hobsortering, når man bruger en hob for prioritetskøen.For sorteringsanvendelsen kan vi betragte svømning og synk direkte, i stedet for at gemme prioritetskøens hobrepræsentation. Hermed kan vi sortere en række uden ekstra pladsforbruge ved at lade hoben blive repræsenteret af den række, vi vil sortere. Hobsortering falder derved i to faser: hobkonstruktion, hvor vi omorganiserer den oprindelige række så den opfylder hobinvarianten, og nedsortering, hvor vi trækker elementerne ud af hoben i faldende ordning for at konstruere det sorterede resultat.
- Hobkonstruktion. Vi er ligetil at konstruere hoben i tid proportional med N lg N ved at arbejde sig gennem rækken fra venstre til højre. Vi bruger svømning til at sikre, at alle indgange til venstre for vores pegefinger udgør til et hobordnet, fuldstændigt træ. Dette svarer til gentagne indsætninger i prioritetskøen. En snedigere metode, der er meget mere effektiv, er at arbejde fra højre til venstre og bruge synk til at skabe delhobe. Betragt hertil en position med en knude, hvis begge børn er hobe. Når knuden synker på plads, vil resultatet være en hob på med rod i knudens oprindelige position.
- Nedsortering. Broderparten af hobsortering sker i den anden fase, hvor vi fjerner maksimumselementer fra hoben og sætter dem på plads i rækkens bagerste indgange, efterhånden som de bliver ledige.
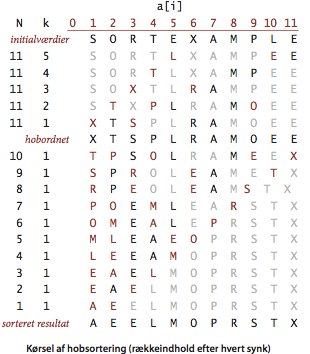
Programmet Heap.java er en fuldstændig
implementation af hobsortering. Forneden vises en kørslel med
rækkeindholdet efter hvert synk.
Påstand.
Synkbaseret hobkonstruktion tager lineær tid.
Påstand.
Hobsortering bruger højst 2N lg N sammenligninger og
ombytninger for at sortere N elementer.
Synk til bunden, swøm op. Floyd observerede i 1964, at de fleste elementer, der sættes ind i hoben under nedsorteringen, synker hele vejen til bunden alligevel. Vi kan derfor spare sammenligninger ved at lade være med at undersøge, om elementet er synket på plads: vi lader det bytte plads med det største af børnene indtil det når bunden. Derefter lader vi det svømme opad i hoben til den korrekte plads. Denne idé halverer asymptotisk antallet af sammenligninger, men kræver til gengæld lidt ekstra bogholderi.
