4.1 Urettede grafer
Urettede grafer.
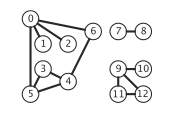
En graf består af en mængde af knuder og en samling af kanter, der hver forbinder to knuder. Vi bruger tallene \(\{0,\ldots, V-1\}\) for at navngive knuderne i en graf med \(V\) knuder.
Glosar.
Vi benytter følgende definitioner og terminologi.- En løkke er en kant der forbinder en knude med sig selv.
- To kanter er parallelle hvis de forbinder samme par af knuder.
- Når en kant forbinder to knuder, kaldes knuderne naboer til hinanden, kanten er nabokant til hver knude og kantens to knuder kaldes for dens endeknuder.
- En knudes grad er antallet af dens nabokanter.
- En delgraf er en delmængde af grafens kanter samt deres endeknuder.
- En sti i en graf er en sekvens af naboknuder. En simpel sti er en sti uden gentagne knuder.
- En kreds er en sti med mindst én kant, hvor stiens første og sidste knude er den samme. En simpel kreds er en kreds uden gentagne knuder, bortset fra stiens første og sidste knude.
- Længden af en sti og en kreds er antallet af kanter.
- En knude er forbundet til en anden knude, hvis der findes en sti indeholdende begge knuder.
- En graf er sammenhængende hvis der er en sti fra hver knude til hver anden knude.
- En usammenhængende graf består af en mængde af sammenhængskomponenter, som udgøres af grafens maksimale, sammenhængende delgrafer.
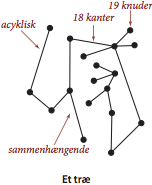
- En acyklisk graf er en graf som ikke indeholder nogen kreds.
- Et træ er en acyklisk, sammenhængende graf.
- En skov er en mængde af knudedisjunkte træer.
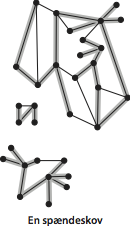
- En sammenhængende grafs spændetræ er en delgraf som er et træ og indeholder alle grafens knuder. En grafs spændeskov en foreningsmængden af dens sammenhængskomponenters spændetræer.
- En todelt graf er en graf hvis knuder kan opdeles i to mængder, således at hver kants endeknuder ligger i hver sin mængde.
Datatype for urettede grafer.
Vi implementerer følgende APG for urettede grafer.
| public class Graph | ||
|---|---|---|
| Graph(int V) | skab en graf med \(V\) knuder og ingen kanter | |
| Graph(In in) | læs en graf fra indputstrømmen in | |
| int | V() | antal knuder |
| int | E() | antal kanter |
| void | addEdge(int v, int w) | tilføj kanten v-w til denne graf |
| Iterable<Integer> | adj(int v) | gennemløb alle naboknuder til \(v\) |
| String | toString() | tekstuel repræsentation af grafen |
Den centrale metode er nabogennemløberen adj(), som tillader klientkoden at gennemløbe alle naboer til en given knude. Bemærkelsesværdigt nok kan vi bygge alle algoritmer i denne sektion ved brug af bare denne centrale mekanisme.
Vores testdata tinyG.txt, mediumG.txt og largeG.txt bruger følgende indputformat:
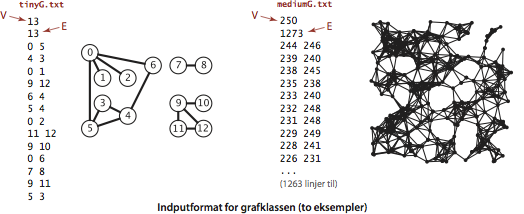
Programmet GraphClient.java er en typisk klient til grafbehandling.
Repræsentation af grafer.
Vi bruger nabolisterepræsentationen af grafer, dvs. at vi opretholder en knude-indekseret række af lister over hver knudes naboknuder.
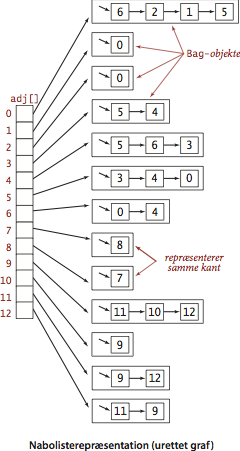
Programmet Graph.java implementer APG’en for urettede grafer ved brug af nabolisterepræsentationen. Programmet AdjMatrixGraph.java implementerer samme APG ved brug af nabomatrixrepræsentationen.
Dybde-først-søgning.
Den klassiske dybde-først-søgning (DFS) er en rekursiv metode som systematisk besøger alle knuder og kanter i en graf. For at besøge en knude,- markér knuden som besøgt,
- besøg rekursivt alle hidtil ubesøgte naboknuder.
| public class Search | ||
|---|---|---|
| Search(Graph G, int s) | find knuder forbundet med startknuden \(s\) | |
| boolean | marked(int v) | er \(v\) forbundet med \(s\)? |
| int | count() | hvor mange knuder er forbundet med \(s\)? |
Finde vej.
Vi udvider nu dybde-først-søgningen til ikke bare at rapportere eksistensen af en vej mellem to givne knuder, men til at finde vejen, forudsat at den findes. Vi vil implementere følgende APG:
| public class Paths | ||
|---|---|---|
| Paths(Graph G, int s) | find knuder forbundet med startknuden \(s\) | |
| boolean | hasPathTo(int v) | er der en vej fra \(s\) til \(v\)? |
| Interabel<Integer> | pathTo(int v) | vej fra \(s\) til \(v\); eller null hvis ingen vej findes |
Hertil husker vi den kant v-w, som for første gang tager os til knuden \(w\), ved at sætte variablen edgeTo[w] til \(v\). Med andre ord er kanten v-w den sidste kant på en vej fra startknuden \(s\) til knuden \(w\). Resultatet af den udvidede dybde-først-søgning er nu et træ med rod i startknuden \(s\); rækken edgeTo[] indeholder en forælderhægtet repræsentation af dette træ. Programmet DepthFirstPaths.java implementerer denne tilgang.
Bredde-først-søgning.
Dybde-først-søgning finder en eller anden vej fra startknuden \(s\) til målknuden \(v\). Ofte ef vi interesserede i en korteste af disse veje, dvs. en vej med et minimalt antal kanter. Bredde-først-søgning (BFS) er den klassiske løsning for denne opgave. For at finde en korteste vej fra startknuden \(s\) til målknuden \(v\), begynder vi i \(s\) og ser om \(v\) findes blandt de knuder, vi kan nå ved at følge bare én kant fra \(s\). begynder vi i \(s\) og ser om \(v\) findes blandt de knuder, vi kan nå ved at følge to kanter fra \(s\), osv.For at implementere denne strategi opretholder vi en kø af alle knuder, som er blevet markeret, men hvis nabolister endnu ikke er blevet undersøgt. Vi begynder med at markere og kø startknuden, og udfører følgende operationer, indtil køen er tom:
- Afkø den næste knude v.
- Markér og kø hver umarkerede naboknude til \(v\).
Sammenhængskomponenter.
Vores næste direkte anvendelse af dybde-først-søgning er at finde grafens sammenhængskomponenter. I afsnit 1.5 så vi, at «hænger sammen med» er en ækvivalensrelation, og at sammenhængskomponenterne svarer til knudemængdens inddeling i ækvivalensklasser. Vi definerer følgende APG:
| public class CC | ||
|---|---|---|
| CC(Graph G) | konstruktøren forbehandler grafen | |
| boolean | connected(int v, int w) | er \(v\) og \(w\) forbundet |
| int | count() | antal sammenhængskomponenter |
| int | id(int v) | komponenet-id for \(v\), et heltal mellem 0 og count()-1 |
Programmet CC.java bruger DFS for at implementere APG’en for sammenhængskomponenter.
Påstand. DFS marker alle knuder forbundet til en given startknude i tid proportional med summen af deres grader. DFS rapporterer en vej fra startknuden til en markeret knude i tid proportional med vejens længde.
Påstand. For knude \(v\), der kan nås fra \(s\), beregner BFS en korteste vej (i antal kanter) fra \(s\) til \(v\). Køretiden for BFS er proportional med \(V + E\) i værste fald.
Påstand. DFS bruger forbehandlingstid og -plads proportional med \(V + E\) for at støtte sammenhængsforespørgsler i konstant tid per forespørgsel.
Flere anvendelser af DFS.
Vi kan bruge dybde-først-søgning til at besvare en række spørgsmål udover de fundamentale anvendelser foroven.- Acyklisk graf: Indeholder grafen en kreds? Programmet Cycle.java bruger DFS for at afgøre om en givet graf indholder en kreds, og rapporterer kredsen i givet fald. Køretiden er proportional med \(V+ E\) i værste fald.
- Tofarvning: Kan hver af grafens knuder tildeles en af to farver, således at ingen kants endeknuder har samme farve? Programmet Bipartite.java bruger DFS til at afgøre om en givet graf kan todeles. I givet fald rapporteres todelingen, ellers rapporteres en kreds af ulige længde. Køretiden er proportional med \(V+ E\) i værste fald.
- Bro: En bro (også kaldet snitkant) er en kant, hvis fjernelse øger antallet af grafens sammenhængskomponenter. Med ande ord er en kant en bro, hvis og kun hvis den ikke ligger på nogen kreds. Programmet Bridge.java bruger DFS til at finde alle broer i en givet grafen. Køretiden er proportional med \(V + E\) i værste fald.
- Tosammenhæng: En artikulationsknude (også kaldt snitknude) er en knude, hvis fjernelse øger antallet af grafens sammenhængskomponenter. En graf uden artikulationsknuder kaldes tosammenhængende. Programmet Biconnected.java bruger DFS for at finde broer og artikulationsknuder. Køretiden er proportional med \(V+ E\) i værste fald.
- Planaritet: En graf er planær, hvis den kan tegnes i planen, således at ingen kanter krydser hinanden. Hopcroft-Tarjan-algoritmen er en avanceret anvendelse af DFS, som afgør om en givet graf er planær i lineær tid.
Symbolgrafer.
I typiske anvendelser udgøres knudenavnene ikke af heltal, men af strenge. Hertil definerer vi et indputformat med følgende egenskaber.- Knudenavne er strenge.
- En specifik grænsestreng separerer knudenavne. Dette muliggør, at knudenavne indeholder blanktegn.
- Hver linje beskriver en mængde af kanter, således at den første knude i hver linje har en kant til hver af de andre knuder i linjen.
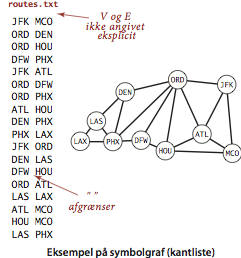
Arkivet routes.txt indeholder et lille eksempel.
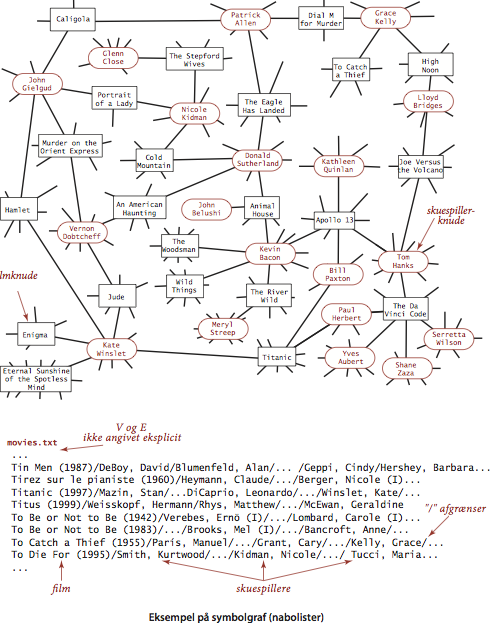
Arkivet movies.txt er et større eksempel fra filmdatabasen Internet Movie Database. Hver linje i indput beskriver en film, efterfulgt af skuespillerne i filmen.
- APG.
Følgende APG bygger en graf ud fra repræsentationen foroven.
public class SymbolGraph SymbolGraph(String filename, String delim) byg grafen beskrevet i arkivet filename; knudenavne er separeret med delim boolean contains(String key) er key en knude? int index(String key) indeks for nøglen key String name(int v) nøglen for indeks \(v\) Graph G() underliggende graf - Implementation.
Programmet SymbolGraph.java implementerer
APG’en.
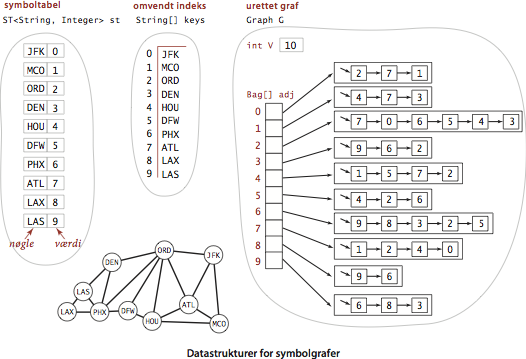
Den bygger tre datastrukturer:
- En symboltabel st med nøgler af strengtypen String (knudenavne) og heltalsværdier int (indices)
- En række af nøgler keys[], som bruges som omvendt indeks til at finde knudenavnet knyttet til hvert heltalsindeks.
- En graf Graph G bygget over knudernes indices.
- Separationsgrad i sociale netværk. Programmet DegreesOfSeparation.java bruger BFS til at bestemme separationsgraden mellem to individer i et socialt netværk, dvs. den korteste afstand mellem knuderne i grafen. Det spiller Kevin Bacon-spillet for skuespiller/film-grafen.