2.2 Flettesortering
I dette afsnit betragter vi algoritmer, hvis grundlæggende operation er fletning: Vi fletter to ordnede sekvenser sammen til én stor ordnet sekvens. Denne operation giver anledning til en enkel rekursiv metode kaldet flettesortering: En række kan sorteres ved at rekursivt sortere hver halvdel for sig og derefter flette resultaterne.

Abstrakt fletning på plads.
Flettemetoden merge(a, lo, mid, hi) i programmet Merge.java lægger resultatet af fletningen af delrækkerne a[lo..mid] og a[mid+1..hi] i én ordnet række a[lo..hi]. Det kunne være ønskværdigt at gennemføre denne proces uden at bruge for meget ekstra plads, men sådanne løsninger er overordentligt komplicerede. I stedet kopierer metoden merge() alting ind en hjælperække under fletningen og flytter siden resultatet tilbage til den oprindelige række.

Rekursiv flettesortering (oppefra og ned).
Programmet Merge.java implementerer rekursiv flettesorting ved brug af den abstrakte fletning på plads. Det er et af de bedst kendte eksemper på anvendelsen af del og hersk-paradigmet til konstruktion af effektive algoritmer.

Påstand.
Flettesortering oppefra og ned bruger mellem \(\frac{1}{2} N\operatorname{lg} N\) og \( N\operatorname{lg} N\) sammenligninger og højst \(6 N\operatorname{lg} N\) rækkeadgange for at sortere en række af længde \(N\).Forbedringer.
Vi kan nedbringe køretiden for flettesortering betydeligt ved hjælp af nogle sindrige modifikationer af implementationen.- Brug indsættelsessortering for små delrækker. Vi kan forbedre tidsforbruget for de fleste rekursive algoritmer ved at behandle de små rekursive instanser separat. Ved at skifte til indsættelsessortering for korte delrækker kan man forbedre køretiden for en typisk implementation af flettesortering med 10 til 15 procent.
- Test om rækken allerede er sorteret. For rækker som i forvejen er sorterede kan vi nedbringe køretiden til lineæar ved at tilføje en test som springer fletningen merge() over, hvis a[mid] <= a[mid+1]. Bemærk at samtlige rekursive kald stadig gennemføres, også på en sorteret række.
- Undgå kopiering af hjælperækken. Man kan undgå tiden (men ikke pladsen) som bruges til at kopiere til og fra hjælperækken ved fletningen. Ideen er at lade den oprindelige række og hjælperækken bytte rolle undervejs i rekursionen. Vi behøver to forskellige udgaver af sorteringsmetoden: Den ene sorterer fra den oprindelige række til hjælperækken, den anden sorterer fra hjælperækken til den oprindelige række. Med nogle fiksfakserier i de rekursive metodekald kan man få sorteringen til at bruge enten den ene eller den anden vej på hvert niveau af rekursionen.
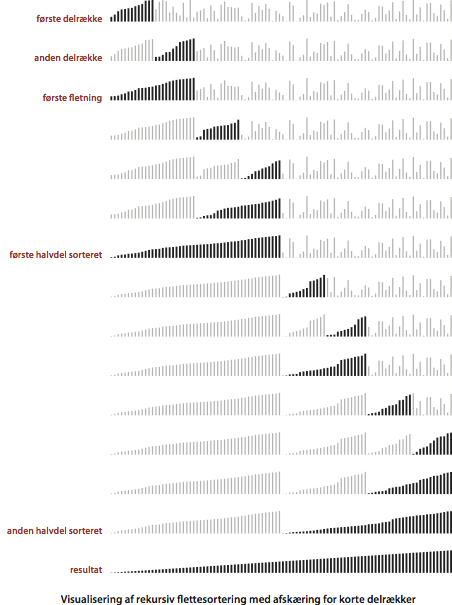
Visualisering.
Programmet MergeBars.java visualiserer opførslen af flettesortering med afskæring for små delrækker.
Iterativ flettesortering (nedefra og op).
Selvom vi tænker på flettesortering som en metode til at sortere store rækker, bliver det meste af tiden under processen brugt til at flette meget korte delrækker. Men det udgangspunkt giver det mening at vende implementationen af flettesortering på hovedet: Først færdiggør vi alle fletninger af rækker af længde 1, som jo ellers ville blive udført, hver gang rekursionen når bunden. Dette skaber \(N/2\) sorterede delrækker af længde 2. I næste gennemløb fletter vi disse delrækker parvist til \(N/4\) sorterede delrækker af længde 4, og så videre indtil vi til sidste fletter hele rækken. Denne metode kan implementeres med endnu mindre kode en den rekursive implementation. Programmet MergeBU.java implementerer iterativ flettesortering.

