2.1 Grundlæggende sortering
I dette afsnit behandles to grundlæggende sorteringsmetoder, udvalgssortering og indsættelsessortering, samt en variation af den ene, shellsortering.
Spillets regler.
Vi betragter algoritmer på rækker af elementer, der hver indeholder en nøgle. Målet er at omarrangere elementerne således at deres nøgler til sidst står i ikke-aftagende ordning. I java konkretiseres nøgler af en indbygget mekanisme: grænsefladen for sammenlignelige elementer, Comparable. Med ganske få undtagelser vil vores kode kun bruge to metoder for at behandle til elementerne: sammenligningsmetoden less(), der afgør om et element er mindre end et andet, og ombytningsmetoden exch(), der bytter plads på to elementer.
private static boolean less(Comparable v, Comparable w) { return (v.compareTo(w) < 0); } private static void exch(Comparable[] a, int i, int j) { Comparable swap = a[i]; a[i] = a[j]; a[j] = swap; }
- Omkostningsmodel for sortering. De kanoniske operationer for sorteringsalgoritmer er antallet af sammenligninger og ombytninger. For de algoritmer, som ikke bruger sammenligning og ombytning, tæller vi i stedet rækkeopslag.
- Ekstra lager. Vi inddeler sorteringsalgoritmerne i to grupper: Dem, der sorterer på plads, dvs. ikke bruger ekstra lager udover XXX stakken af funktionskald og et konstant antal instansvariabler, og dem, der bruger ekstra lager til at håndtere en kopi af den række, der skal sorteres.
- Datatyper. Vores kode virker for alle datatyper, der implementerer javas sammenligningsgrænseflade Comparable. Det inkluderer javas numeriske pakketyper som fx Integer og Double, men også strengtypen String og diverse mere komplicerede typer som File, URL og Date. Grænsefladen kræver, at typen implementer en sammenligninsmetode compareTo(), således at v.compareTo(w) returnerer henholdsvist et negativt heltal hvis \(v < w\); nul hvis \(v = w\) og et positivt heltal hvis \(v > w\). Datatypen definerer således en total ordning givet ved \(v \leq w\) hvis v.compareTo((Object)w) <= 0. En total ordning opfylder følgende krav:
- Refleksivitet: For alle \(v\) gælder \(v \leq v\).
- Antisymmetri: For alle \(v\) og \(w\) gælder, at \(v \leq w\) og \(w \leq v) medfører \(v = w\).
- Transitivitet: for alle \(v\), \(w\) og \(x\) gælder, at \(v \leq w\) og \(w \leq x\) medfører \(v \leq x\).
Derudover skaber v.compareTo(w) en undtagelse hvis v og w er inkompatible typer, eller hvis nogen af dem har værdien null.
Datumstypen Date.java viser, hvordan man implementerer sammenligningsgrænsefladen Comparable for en brugerdefineret datatype.
Udvalgssortering.
En af de enkleste sorteringsalgoritmer virker som følger: Begynd med at finde det mindste element i rækken, og lad det bytte plads med rækkens første element. Fortsæt med at finde det næstmindste element og lad det bytte plads med rækkens andet element. Fortsæt indtil hele rækken er sorteret. Denne algoritme kaldes udvalgssortering, fordi den hele tiden vælger det mindste, tilbageværende element. Programmet Selection.java implementer denne algoritme.
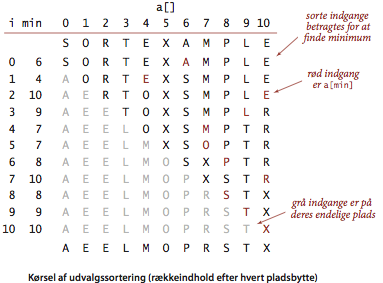
Påstand.
Udvalgssortering bruger \(\sim~N^2/2\) sammenligninger og \(N\) ombytninger for at sortere en række af længde \(N\).Indsættelsessortering.
Den algoritme, kortspillere typisk bruger til at sortere kortene på hånden, er at betragte kortene et efter et og putte dem på deres rette plads bland de allerede behandlede kort. For at implementere dette i en række, skal vi skabe plads for det nye element ved at flytte de større elementer en position til højre inden vi kan sætte det nye element på den nu ledige plads. Programmet Insertion.java implementerer denne metode, som kaldes indsættelsessortering.
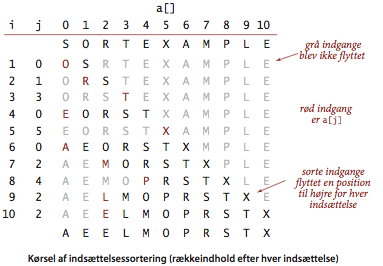
Påstand.
For en række af længde \(N\) som indeholder forskellige nøgler i uniformt tilfældig orden, bruger indsættelsesortering i gennemsnit \(\sim N^2/4\) sammenligninger og \(\sim N^2/4\) ombytninger. I værste flad bruges \(\sim N^2/2\) sammenligninger og \(\sim N^2/2\) ombytninger. I bedste fald bruges \(N-1\) sammenligninger og ingen ombytninger.Indsættelsessortering virker udmærket for visse typer af ikke-tilfældige rækker, som man ofte møder i praksis, sågar hvis N er enorm. En inversion er et par af nøgler i uorden. For eksempel er der 11 inversioner i E X A M P L E, nemlig E-A, X-A, X-M, X-P, X-L, X-E, M-L, M-E, P-L, P-E og L-E. En række kaldes delvis sorteret, hvis antallet af inversioner i rækken er mindre en et konstant multiplum af rækkestørrelsen.
Påstand.
Antallet af ombytninger ved indsættelsessortering er lig med antallet af inversioner i rækken. Antallet af sammenligninger er mindst antallet af inversioner og højst antallet af inversioner plus rækkestørrelsen.Egenskab.
For rækker af forskellige nøgler i uniformt tilfældig orden er køretiderne af indsættelsessortering og udvalssortering kvadratiske og inden for en lille konstant faktor af hinanden.Programmet SortCompare.java bruger sorteringsmetoden sort() i to i kommandolinjen angivne sorteringsalgoritmer til at gennemføre et antal eksperimenter (sortering af tilfældige rækker af given størrelse) og skriver forholdet mellem de observerede køretider.
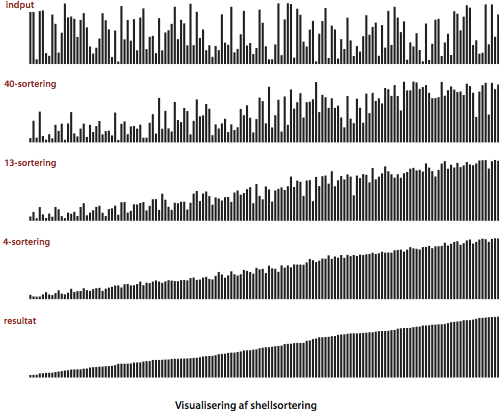
Visualisering af sorteringsalgoritmer.
Vi benytter en enkel visuel repræsentation for at synliggøre sorteringsalgoritmernes opførsel. Vi tegner rækkernes indhold som vertikale søjler, som skal sorteres efter deres højde. Programmerne SelectionBars.java og InsertionBars.java producerer disse visualiseringer.
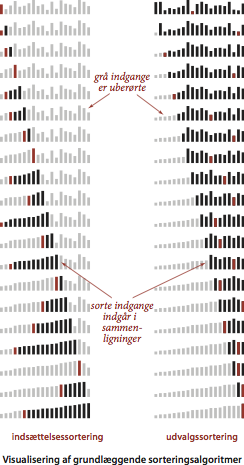
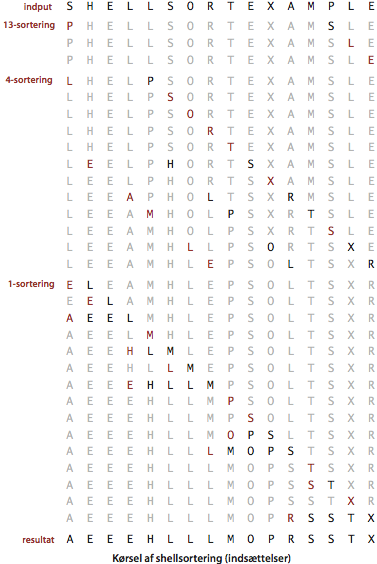
Shellsortering.
Shellsortering er en enkel udvidelse af indsættelsessortering opkaldt efter Donald Shell, som beskrev metoden i 1959. Shellsortering tillader ombytning af elementer som står langt fra hinanden i rækken, hvilket skaber delvist sorterede rækker, der til sidst indsættelsessorteres. Givet et heltal h kaldes en sekvens h-sorteret, hvis alle delsekvenser bestående af hvert hte element er sorteret. En sorteret sekvens her h-sorteret for h=1.