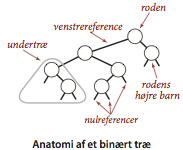
3.2 Binære søgetræer
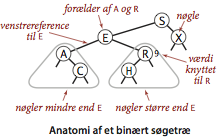
Vi betragter nu en implementation af symboltabeller som kombinerer fleksibiliteten af indsættelse i en hægtet liste med effektiviteten af søgning i en ordnet række. Ved at bruge to henvisninger per knude kan vi implementere symboltabeller i et binært søgeræ, som er en af datalogiens mest grundlæggende datastrukturer.Definition (søgetræsinvariant). Et binært søgetræ (BST) er et binært træ, hvor hver knude indeholder en sammenlignelig nøgle og en tilknyttet værdi, således at hver knudes nøgle er større end nøglerne i knudens venstre undertræ og mindre end nøglerne i knudens højre undertræ.
Grundlæggende implementation.
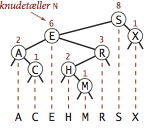
Programmet BST.java implementerer APG’en for ordnede symboltabeller ved brug af et binært søgetræ. Vi definerer in privat, indre klasse for træets knuder. Hver knude indeholder en nøgle, en tilknyttet værdi, henvisninger til venstre og højre undertræ og en knudetæller. Venstre henvisning beger på et BST af elementer med mindre nøgler, og højre henvisning peger på et BST af elementer med større nøgler. Instansvariablen N angiver antallet af knuder i undertræet rodfæstet ved knuden. Vi vil se forneden, hvordan dette felt muliggør implementationen af diverse ordningsrelaterede symboltabelsoperationer.
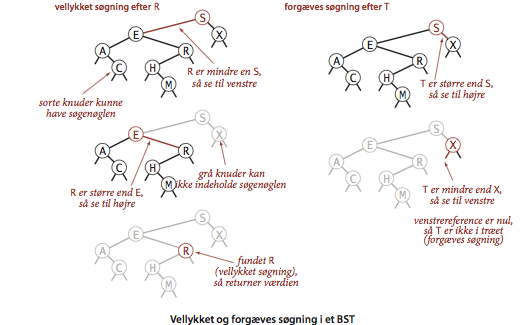
- Søgning.
Søgetræets rekursive struktur giver direkte anledning til en rekursiv
algoritme for at lede efter en nøgle i træet: Hvis træet er tomt,
finder vi ikke nøglen.
Hvis nøglen findes i træets rod, returnerer vi rodknudens værdi.
Ellers søger vi rekursivt i venstre eller højre undertræ, afhængigt af
søgenøglens og rodnøglens indbyrdes værdi.
Det rekursive metode get() implementer denne algoritme
direkte.
Det tager en knude som første argument, som angiver undertræets rod,
og en nøgle som andet argument; og kaldes med rodknuden og søgenøglen
som argumenter.
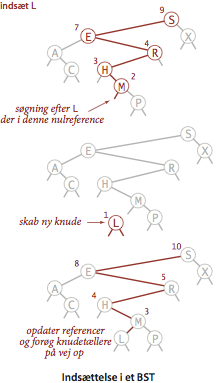
- Indsættelse.
Indsættelse i et BST er ikke meget vanskeligere at implementere end
søgning.
Forgæves søgning efter en nøgle ender i en nulreference; denne
reference skal nu blot erstattes med en reference til en ny knude
med det indsatte nøgle-værdi-par.
Den rekursive metode put() implementerer dette i samme stil
som for den rekursive søgning: Hvis træet er tomt, returneres en ny
knude med den indsatte nøgle og værdi.
Hvis søgenøglen er mindre end rodknudens nøgle, sættes venstre
henvisning til resultatet af indsættelse i venstre deltræ, ellers
sættes højre henvisning til resultatet af indsættelse i højre deltræ.
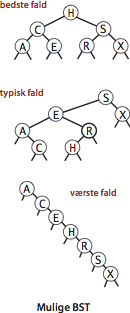
Analyse.
Køretiden for algoritmer på binære søgetræer afhænger af træets form, som igen afhænger af rækkefølgen af nøgleindsættelser.
Påstand.
En vellykket søgning i et binært søgetræ af \(N\) uniformt tilfældige nøgler bruger ~\( 2 \ln N\) (omtrent \(1.39 \operatorname{lg} N\)) sammenligninger i gennemsnit.Påstand.
Insættelse og forgæves søgning i et binært søgetræ af \(N\) uniformt tilfældige nøgler bruger ~ \(2 \ln N\) (omtrent \(1.39 \operatorname{lg} N\)) sammenligninger i gennemsnit.
Ordningsbaserede metoder og fjernelse.
Binære søgetræer opretholder søgenøglerne i orden. Derfor kan vi implementere metoderne fra programmeringsgrænsefladen for ordnede symboltabeller.- Minimum og maksimum. Hvis rodens venstre undertræ er nulreferencen, så er søgetræets mindste nøgle i roden. Ellers er søgetræets mindste nøgle i venstre undertræ. På samme måde er søgetræets største nøgle i højre undertræ.
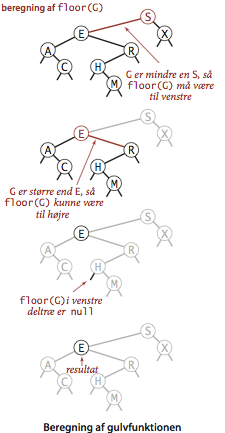
- Gulv og loft. Hvis søgenøglen er mindre en træets rodnøgle, så er søgenøglens gulv (dvs. symboltabellens største nøgle mindre end søgenøglen) i venstre undertræ. Hvis søgenøglen er større end rodnøglen, så kan søgenøglens gulv findes i højre undertræ, men kun hvis dette indeholder en nøgle, der er mindre end eller lig med søgenøglen. I modsat fald, eller hvis søgenøglen er lig med rodnøglen, er rodnøglen netop søgenøglens gulv. Loftet findes på lignende måde, ved at bytte om på højre og venstre.
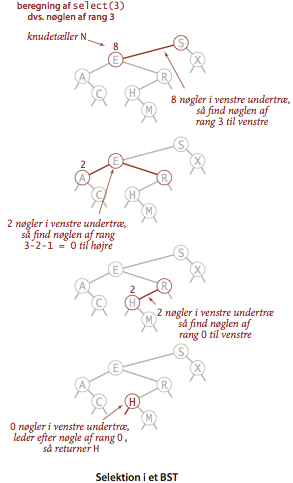
- Selektion.
Antag, at vi søger nøglen af rang \(k\), dvs.
den nøgle, der er større end nøjagtig \(k\) andre nøgler i det
binære søgetræ.
Lad \(t\) betegne antallet af nøgler i rodens venstre undertræ.
Hvis \(t>k\), så søger vi rekursivt efter nøglen af rang \(k\) i
venstre undertræ.
Hvis \(t=k\), så returnerer vi rodnøglen.
Hvis \(t
- Rangering. Hvis den givne nøgle er lig med rodnøglen, returnerer vi antallet af nøgler \(t\) i venstre undertræ. Hvis den givne nøgle er skarpt mindre end rodnøglen returnerer vi den givne nøgles rang i venstre undertræ. Hvis den givne nøgle er større end rodnøglen, så returnerer vi \(t\) plus 1 (for a tælle rodnøglen) plus den givne nøgles rang i højre undertræ.
- Fjernelse af maksimum og minimum. For at fjerne den mindste nøgle i træet, følger vi venstrereferencer, indtil vi finder en knude med en venstre nulreference. Vi erstatter forælderns reference til denne knude med knudens højrereference. Fjernelse af maksimum foregår symmetrisk.
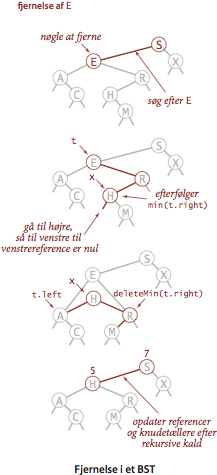
- Fjernelse. Fjernelse af en vilkårlig knude med et eller ingen børn foregår på samme måde som for minimum og maksimum. Men hvordan fjerner man en knude med to børn? Vi står med to referencer, men forælderknuden har kun plads til den ene. Løsningen til dette dilemma blev første gang foreslået af T. Hibbard i 1962. Fjern knuden x ved at erstatte den med sin efterfølger i nøgleordningen. Fordi x har et højrebarn, må dens efterfølger være knuden med den mindste nøgle i x’s højre deltræ. Erstatningen bevarer træets ordning, fordi der ikke kan findes nøgler mellem x.key og dens efterfølgers nøgle. Vi kan erstatte
x med dens efterfølger i blot fire enkle skridt: - Lad t henvise til den knude, som skal fjernes.
- Lad x henvise til sin efterfølger min(t.right).
- Sæt x’s højrerefernce (som jo skal pege på det binære søgetræ af nøgler større end x.key) til resultatet af deleteMin(t.right)
- Sæt x’s venstrereference (som var nulreferencen) til t.left, som jo peger på alle nøgler mindre end både den fjernede nogle og dens efterfølger.
Denne metode bevarer søgetræsinvarianten, men har den ulempe, at der kan opstå køretidsproblemer i nogle praktiske situationer. Problemet er, at konventionen om at erstatte x med dens efterfølger er vilkårligt og usymmetrisk: Hvorfor ikke vælge forgængeren i stedet for?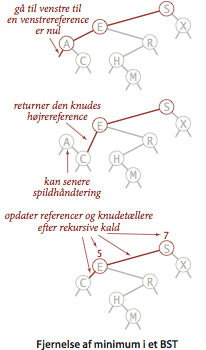
- Intervalsøgning. For at implementere gennemløbsmedtoden keys(), der skal returnere nøgler i et givet interval, begynder vi med en grundlæggende rekursiv metode for gennemløb af et BST, kaldet indordensgennemløb. For at illustrere metoden, betragter vi opgaven at skrive alle nøgler i et BST i sorteret rækkefølge. Hertil skriver vi først rekursivt nøglerne i venstre undertræ, som jo alle er mindre en rodnøglen ifølge søgetræsinvarianten. Så skriver vi rodnøglen. Siden skriver vi rekursivt nøglerne i højre undertræ, som jo alle er større end rodnøglen ifølge søgetræsinvarianten.
private void print(Node x) { if (x == null) return; print(x.left); StdOut.println(x.key); print(x.right); }For at implementere gennemløbsmetoden keys() med to argumenter modificerer vi koden således at vi stiller hver nøgle i intervallet i en kø og undgår de rekursive kald til undertræer, der ikke kan indholde nøgler i det givne interval.